|
|
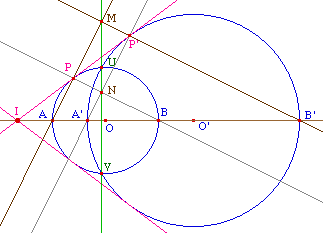
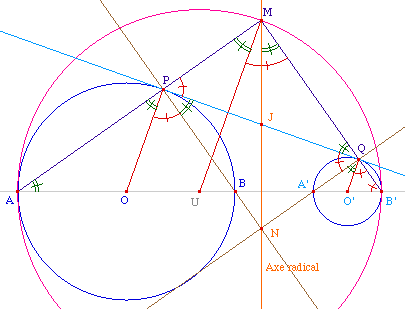
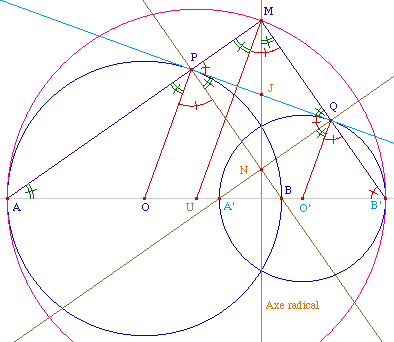
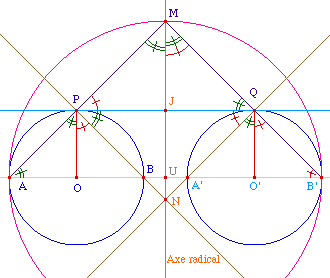
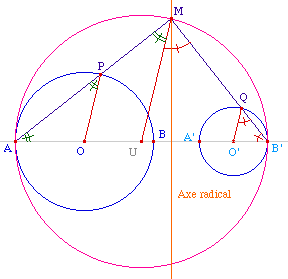
Soient donc deux cercles non
concentriques de centre O et O', le premier coupe la droite
des centres en A et B le second, selon la même
orientation, en A' et B'. Sauf si l'un des cercles est
à l'intérieur de l'autre - et dans ce cas il
n'y a pas lieu de chercher de tangentes communes
extérieures, elles n'existent pas - l'axe radical est
entre A et B' et coupe donc le cercle de diamètre
[AB']. Soit U le centre de ce cercle et M l'un de
ses intersections avec l'axe radical.
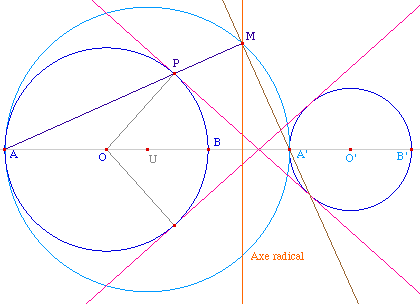
Le triangle AMB' est rectangle en
M et U est le milieu de l'hypothénuse, donc AUM est
isocèle en U. Dans le triangle AUM la
parallèle à (UM) passant par O coupe
[AM] en P. Par homothétie le triangle AOP est
aussi isocèle, et donc OP = OA c'est-à-dire
que P est l'intersection du segment [AM] avec le
cercle de centre O.
De même pour le point Q
intersection du segment [MB'] et de la
parallèle à (UM) passant par O'. Pour les
mêmes raisons, Q est en fait l'intersection du segment
[MB'] et du cercle de centre O'. Et ainsi (OP) //
(O'Q).
|