[Retour Géométrie vectorielle] [Menu général]
|
|
|
|
|
|
|
|
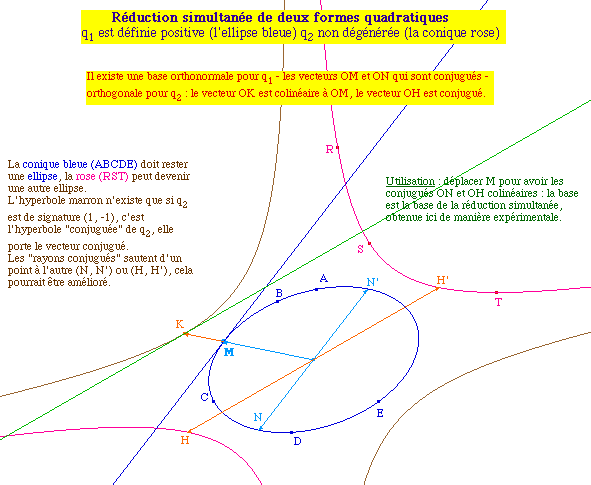
Du moins en théoriqe (illustration de gauche).Mais, compte tenu des difficultés de la version actuelle de Cabri (09/98) sur le suivi des intersections avec les coniques - essentiellement lors du changement de type - on a pris ici comme axe la droite passant par O et le milieu de [MN], ce qui donne un résultat plus fiable - à droite - que les parallèles aux côtés.
|
|
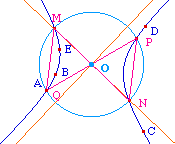 |
Reste que cette solution n'est pas idéale non plus, comme on le voir ci-contre.D'autres approches plus fines, utilisant des arcs de cercles par exemple ne sont pas nécessairement plus fiable.Cette construction a le mérite d'être élémentaire et - compte tenu de l'algorithme actuel d'intersection - de rester fiable sur les ellipses par exemple.Rappelons que la méthode utilisant le point de Frégier d'un point donne bien les deux axes d'une conique dans tous les cas. |


Cas d'une seconde forme quadratique définie positive

Réalisation d'une réduction
simultanée en dehors des hypothèses
générales du théorème.
![]() DiagSim3.fig
DiagSim3.fig