Problem by Peter Ash (geometry forum 12 April 2006)

Let P be a point on a circle with center O, and let Q be a point on ray OP, with OQ > OP. Let R and S be the points where the tangents from Q intersect the circle, and let T and U be the midpoints of the segments RQ and SQ. Find the locus traced out by T and U, as Q moves.
The curve looks something like y = x⁴. Does it have a name? Can anyone find a simple form of the equation for the curve?

Solution

Equation is obtained using the locus equation feature of Cabri-Geometry II Plus.
The figure is built like the Luigi Tomasi's example in geometry forum:
the circle has equation: x²+y²=1, and the point P has coordinates (0; 1).

Click thumbnail image:

Calculating the equation (by François Rideau and Michel Tixier).
Choose parameter t so that R coordinates are R(sin(t);cos(t)). So Q( 0;1/cos(t)) and T( (1/2) sin(t);(1/2)( cos(t) + 1/cos(t)) )
Then elimination of t via sin(t)² + cos(t)² = 1 gives cartesian equation 4x⁴ + 4x².y² - 4x² - y² + 1 = 0

Alternate cartesian equation (by Michel Tixier):
y = (1-2x²) / √(1 - 4 x²) with x in ] -1/2 , 1/2 [.
x = ±1/2 are two asymptotes of the curve.

Changing radius r = OP for 1,2,3,4,... we can "deduce" with Cabri the general formula:
4x⁴ + 4x².y² - 4r².x² - r². y² + r⁴ = 0
Calculating equation as above confirms this result.

Up to our knowledge this curve has not got a special name.
Jean-Marie Laborde proposes a generalization : what happens if you choose another point than the midpoint, e.g. a point at a constant ratio on QR ?
Joseph Hormière found in the case r = 1 the equation x⁴ + x².y²– 2k.x²– k².y² + k² = 0 where k is the ratio (k=1/2 gives Peter Ash's case).

François Rideau proposes another problem: the construction of the tangent to the quartic at point T .
This problem is difficult from the mathematical point of view and the confirmation with Cabri is amazing.
Here is the François Rideau's figure:

Figure (QuartiqueFR.fig) in French

Figure (QuarticFR.fig) in English

Other loci can be constructed thanks to F. Rideau's figure. The pedal of the nephroïd is a rose:

Figure (Rosace.fig) in French

Figure (Rose.fig) in English

The pedal of the quartic is a non-regular quadrifolium (four-leafed rose):

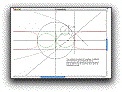
Figure (PodaireJB.fig) in French

Figure (PedalJB.fig) in English

NB Downloading Cabri geometry figures : if your web navigator do not recognize Cabri files, you can use local popup menu for downloading (Windows: right button, MacOS : ctrl-button).