Problem proposed by Peter Ash (geometry forum 12 April 2006)
Let P be a point on a circle with center O, and let Q be a point on ray OP,
with OQ > OP. Let R and S be the points where the tangents from Q intersect
the circle, and let T and U be the midpoints of the segments RQ and SQ. Find
the locus traced out by T and U, as Q moves.
The curve looks something like y = x4. Does it have a name? Can anyone
find a simple form of the equation for the curve?
Solutions (both with Cabri -Geometry and calculating the equation)
Equation is obtained using the locus equation feature of Cabri-Geometry II Plus.
The figure is built like the Luigi Tomasi's example in geometry forum:
the circle has equation: x2+y2=1, and the
point P has coordinates (1; 0).
Locus and equation: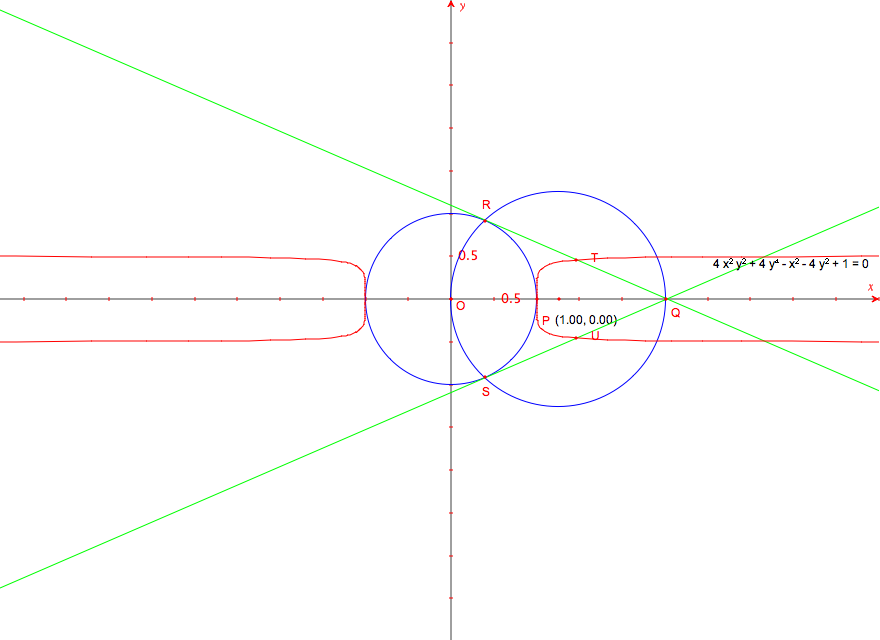
Calculating the equation (by François Rideau and Michel
Tixier) with P (0;1)
Choose parameter t so that R coordinates are R(sin(t);cos(t)). So Q( 0;1/cos(t))
and T( (1/2) sin(t);(1/2)( cos(t) + 1/cos(t)) )
Then elimination of t via sin(t)2 + cos(t)2 = 1 gives
cartesian equation 4x4 + 4x2.y2
- 4x2 - y2 + 1 = 0
Alternate cartesian equation (by Michel Tixier):
y = (1-2x2) / √(1 - 4 x2) with x in ] -1/2 , 1/2
[.
x = ±1/2 are two asymptotes of the curve.
Changing radius r = OP for 1,2,3,4,... we can "deduce" with Cabri
the general formula:
4x4 + 4x2.y2 - 4r2.x2
- r2. y2 + r4 = 0
Calculating equation as above confirms this result.
Up to our knowledge this curve has not got a special name.
Jean-Marie Laborde proposes a generalization : what happens if you choose
another point than the midpoint, e.g. a point at a constant ratio on QR
?
Joseph Hormière found in the case r = 1 the equation x4 +
x2.y2– 2k.x2– k2.y2
+ k2 = 0 where k is the ratio (k=1/2 gives Peter Ash's case).
François Rideau proposed another problem : the construction of the
tangent to the quartic at point T >>>.