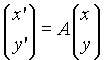Cabri Géomètre dans les Systèmes Dynamiques 

A l'aide du logiciel Cabri Géomètre nous visualisons certaines propriétés qualitatives des systèmes dynamiques, linéaires, à coefficients constants, dans le plan que nous écrirons sous la forme
 
 

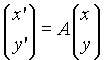       (SD)

Expression dans laquelle x, y sont deux fonctions réelles, de variable réelle t, à déterminer. x' et y' désignent les dérivées par rapport à t de x et y respectivement. A est la matrice du système ( ses éléments sont supposés réels constants).

Rappelons que l'ensemble des solutions est un espace vectoriel sur IR de dimension 2, et que par orbite d'une solution nous entendons la trace de cette solution dans le plan (dit des phases identifié à) IR ².

Il est bien connu que le système (SD) est (topologiquement) équivalent à sa forme canonique de Jordan associée et par suite possède la même analyse qualitative que cette forme (cela vient du fait que les valeurs propres dans les deux formes sont les mêmes). De ce fait nous allons donc supposer, par souci de simplicité et de clarté dans les notations, que le système (SD) est déjà réduit et mis sous la forme canonique de Jordan.

Rappelons d'abord l'expression, en fonction des valeurs propres de la matrice A, d'une solution de (SD) passant par un point

 M =  du plan

 

1.  Cas de deux valeurs propres r, s réelles distinctes 

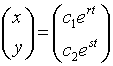
2.  Cas d'une valeur propre, r, double 

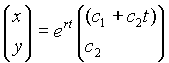
3.  Cas d'une valeur propre complexe de partie réelle r et de partie imaginaire s

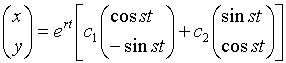
    A l'aide de la calculatrice de Cabri, construire dans le plan des phases, le point P(t) ayant pour composantes x(t) et y(t) dont l'expression est rappelée ci-dessus

Fig.1 : plan des phases

A titre de remarque, signalons qu'on s'est servi du plan des phases pour représenter, aussi, les paramètres r et s du système, la condition initiale M ainsi que la variable indépendante t.

    A l'aide des outils Cabri examiner les points suivants
 

• Pour r et s fixés, produire l'orbite à l'écran comme trajectoire du point P(t) et cela de deux manières (différentes): d'abord par l'outil "lieu" tracer le lieu géométrique des points P(t) quand t parcourt une partie de IR (Fig. 2a), ensuite l'obtenir par l'outil "animation" en déplaçant (par la souris) le point t sur une partie de IR (Fig. 2c) ou par déplacement du point M sur une partie du plan (Fig. 2b).

Fig. 2a	Fig. 2b	Fig. 2c

• Pour r et s fixés, visualiser un faisceau d'orbites correspondant à diverses conditions initiales M (la figure 3 illustre le cas d'un faisceau d'orbites du même genre que celle de la Fig. 2a).

Fig. 3

• Produire une vérification (au sens Cabri) de l'unicité de la solution du problème de Cauchy (indication: construire deux orbites associées respectivement à deux conditions initiales M et M', ramener le point M' sur le point M et constater la superposition des deux orbites).
• Pour r, s et t fixés, produire (par l'outil lieu ou trace) l'ensemble des positions du point P(t) quand on fait varier la condition initiale M (sur une droite ou un cercle par exemple) et confirmer l'allure de l'ensemble des P(t) obtenus par un autre argument (celui de l'image d'une droite ou d'un cercle par une application linéaire).
• Si P(t,M) dénote le point de l'orbite à l'instant t = t₁+t₂ (que certains appellent l'état du processus à l'instant t) correspondant à la condition initiale M, vérifier (au sens Cabri) que

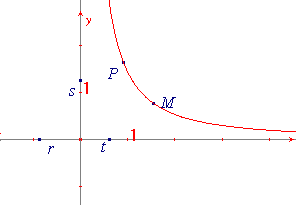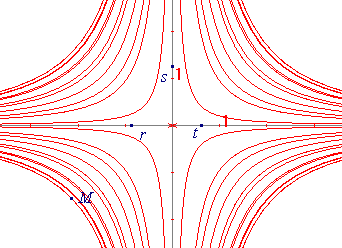
   P(t,M) = P(t2,P(t1,M))

• Générer, instantanément, les orbites du système quand on fait varier (par la souris) ses paramètres r et s et indiquer le type de classe de similitude correspondante (quelques exemples sont illustrés par les figures 4a, 4b et 4c)

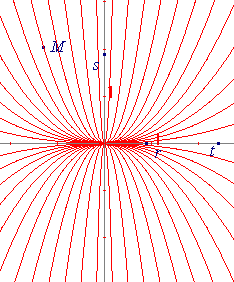Fig. 4a

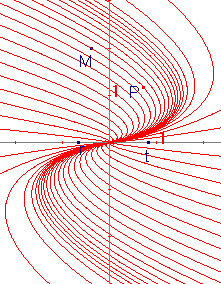Fig. 4b

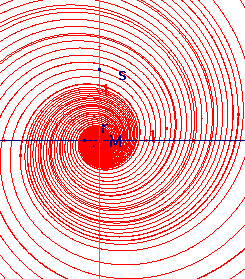Fig.4c

• Visualiser la stabilité ou la non stabilité des solutions selon le signe de r et s (pour la stabilité asymtotique c'est plus simple, il suffit de déplacer le point t de gauche à droite en veillant à ce qu'il reste à droite de 0 et de constater que le point générique P(t) de l'orbite se rapproche de l'origine).
• Construire l'image du point P(t) par une transformation non singulière S du plan, produire les lieux des points P(t) et S(P(t)) et constater la déformation qui en résulte sur les orbites (les figures 5a et 5b illustrent le cas d'une orbite circulaire transformée en ellipse).

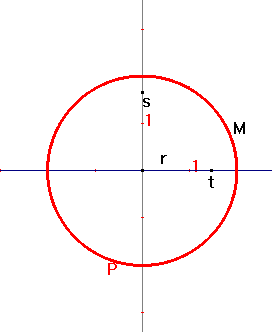Fig.5a

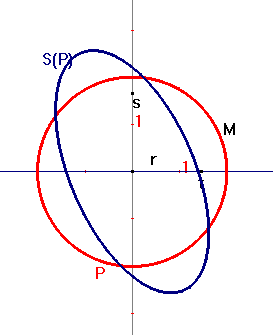Fig.5b

Télécharger des figures Cabri, pour étudier les cas non présentés.
Si besoin, télécharger aussi la version démo de Cabri II.

Ce travail est réalisé dans l'Èquipe IAM du Laboratoire Leibniz de l'IMAG au cours d'un stage de formation continue. Je tiens à remercier tous les membres de cette sympathique équipe pour leurs suggestions et leurs remarques constructives.