2 - Cercle principal et tangentes
[1
- Macro de base - Premières
propriétés] [3
- Applications immédiates]
[Retour Présentation
"Bifocale"] [Retour
Coniques] [Exemples
d'utilisations]
|
|
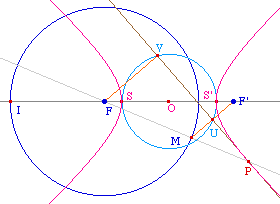
Etant donnés un point F' et un cercle C de centre F, on considère la conique ainsi définie par foyer et cercle directeur. L'homothétie de centre F' de rapport 1/2 transforme le cercle C en un cercle dit principal.Le cercle principal a pour centre celui de la conique et passe par les sommets de la coniques (intersection de l'axe focal et de la conique).La tangente en P étant la médiatrice de [F'M], l'homothétique de M est un point U, de la tangente, mais aussi du cercle principal :Les foyers d'une conique à centre se projettent orthogonalement sur les tangentes en des points appartenant au cercle principal de la conique. |
|
|
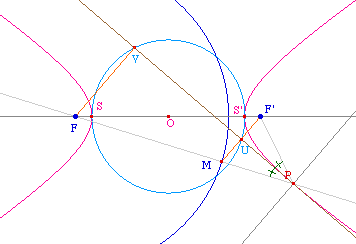
Par ailleurs, puisque la tangente en P est la médiatrice de [F'M], cette tangente est bissectrice de l'angle de FPF'.On a déjà remarqué dans une construction de la page précédente que les vecteurs PF et PM sont R--colinéaires dans le cas de l'ellipse, la tangente est donc une bissectrice extérieure de l'angle FPF', c'est alors la normale qui est la bissectrice intérieure :La normale en un point P d'une ellipse de foyers F et F' est bissectrice intérieure de l'angle FPF'. |
|
|
Etant donné un point P on veut construire les tangentes issues de P à une conique définie par foyer F et cercle directeur associé. On commence par construire le cercle principal.On sait que le foyer se projette orthogonalement sur la tangente en un point du cercle principal. Donc la projection orthogonale du foyer F sur les tangentes issues de P est à l'intersection du cercle principal et du cercle de diamètre [PF]. Soient T1 et T2 ces deux points. Les tangentes sont donc les droites (PT1) et (PT2).La construction des points de contact C1 et C2 des tangentes et de la conique se fait par l'utilisation des deux cercles directeurs : M1 est le symétrique de F par rapport à (PT1) et M2 celui de F' par rapport à (PT2). M2 appartient à l'autre cercle directeur, centré en F. |
|
|
La construction précédente a été faite pour illutrer que la détermination des points de contacts est réalisable à la règle et au compas.Avec la macro disponible en haut de page, on peut ajouter la conique définie par le foyer et le cercle directeur.
|
[1
- Macro de base - Premières
propriétés] [3
- Applications immédiates]
[Retour Présentation
"Bifocale"] [Retour
Coniques] [Exemples
d'utilisations]