Exemples d'utilisation
1 - Cercle circonscrit et cercle
d'Euler
[2
- Conique définie par cercle principal et deux tangentes
]
[3 - Lieu du second foyer des
coniques connaissant un foyer, une tangente un point
]
[Retour Présentation
"Bifocale"] [Retour
Coniques] [Exercices
sur l'approche "bifocale"]
On suppose connus quelques
résultats sur l'orthocentre H d'un triangle ABC. Par exemple
:
Les symétriques de H par
rapport aux droites (AB), (AC) et (BC) appartiennent au cercle
circonscrit du triangle (soit O son centre).
Le milieu de [OH] est le
centre du cercle d'Euler, cercle passant par les pieds
HA, HB, HC des hauteurs issues
respectivement de A, B, et C.
Le cercle d'Euler a pour rayon la
moitié du cercle circonscrit, ainsi le cercle d'Euler
est-il l'homothétique du cercle ciconscrit dans
l'homothétie de centre H et de rapport 1/2.
O et H foyers d'une conique tritangente au
triangle.
|

|
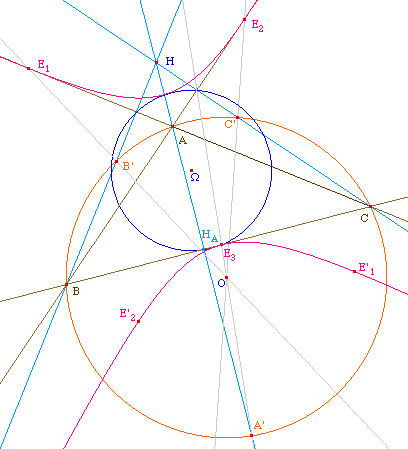
Considérons la conique de
foyer H et de cercle directeur le cercle circonscrit au
triangle ABC, de centre O. Puisque les hauteurs (AH), (BH)
et (CH) coupent ce cercle en des points A', B', et C'
symétriques de H respectivement par rapport aux
droites (BC), (AC) et (AB), ces trois points permettent de
construire les points de la conique en lesquels les
côtés (au sens large) du triangle seront
tangents à la conique.
On construit ainsi E1
intersection de (OB') et (AC), de même E2
et E3. Puisque le centre du cercle d'Euler est le
milieu des deux foyers O et H, c'est le centre de la
conique, on peut donc construire deux autres points de la
conique E'1 et E'2 par
symétrique de E1 et E2. Et
ainsi construire la conique.
Elle est donc tritangente aux
côtés du triangle. Elle a pour cercle
principal, l'homothétique du cercle circonscrit dans
l'homothétie de centre H et de rapport 1/2, soit, le
cercle d'Euler.
Ci contre : cas de
l'ellipse
|
Cas de
l'hyperbole
Remarque : Il
est clair que si le triangle est rectangle, la conique n'est pas
définie, s'il est équilatéral, la conique
construite n'est rien d'autre que le cercle d'Euler,
c'est-à-dire le cercle inscrit dans ce cas. D'une
manière générale nous excluerons dans la suite
ces cas particuliers.
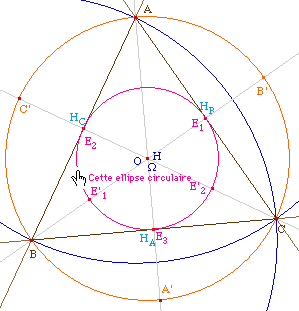
Cas où le triangle est
équilatéral
 La
figure EulerTEq.fig
de ce cas particulier.
La
figure EulerTEq.fig
de ce cas particulier.
Droites de Simpson et de Steiner
associées aux points de contact
Rappels : Soient ABC u triangle et M un
point du plan.
Les projetés orthogonaux
de M sur les droites (AB), (AC) et (BC) sont alignés si et
seulement si M appartient au cercle circonscrit à
ABC.
De même pour les
symétriques par rapport aux droites.
Dans le premier cas on parle de la droite
de Simpson associée à M, relative au triangle ABC, dans
le second cas, de la droite de Steiner. On passe de la
première à la seconnde par une homothétie de
centre M et de rapport 2. La droite de Steiner passe par
l'orthocentre du triangle (cette dernière
propriété ne servira pas en soi ici).
|
|
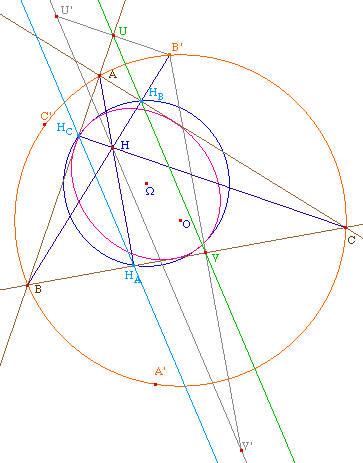
On s'intéresse ici aux
droites de Steiner et de Simpson des points A', B', C' du
cercle circonscrit à ABC qui permettent la
construction des points de contact E1,
E2 et E3 de la conique avec le
triangle. Dans l'illustration ci-dessous, on a tracé
les droites pour le point B' : U et V sont les projections
orthogonales de B' sur (AB) et (BC). Ces points sont donc
alignés avec HB la projection orthogonale
de B' sur (AC).
De même, en notant U' et V'
les symétriques de B' par rapport aux droites (AB) et
(BC), ces points sont alignés avec H - l'orthocentre
- qui est aussi le symétrique de B' par rapport
à (AC).
On constate que la droite de
Steiner de B' est paralléle au côté
opposé [HCHA] du
triangle orthique HAHBHC de
ABC. En effet, l'homothétie de centre B qui envoie H
sur B', envoie aussi - par conservation de
l'orthogonalité - HC sur U et
HA sur V, donc (UV) et
(HCHA) sont bien parallèles.
Nous avons ainsi le résultat suivant :
Les droites de Steiner des
points A', B', C' symétriques de l'orthocentre par
rapport aux côtés du triangle sont
respectivement parallèles au côté
opposé associé du triangle
orthique.
Nous nous proposons maintenant de voir que
l'intersection d'une telle droite de Steiner avec le
côté correspondant du triangle est un point de
la directrice de la conique : par exemple dans
l'illustration ci-dessus la droite de Steiner de B' coupe
(AC) en un point de la directrice de la conique
associée à H.
|
Directrices de la conique
Rappels
: Étant donnés une conique de foyer F, et une tangente
T à la conique en un point A, la tangente coupe la
perpendiculaire en F à [AF] en un point de la
directrice associée au foyer.
Ainsi, pour montrer la propriété
évoquée ci-dessus, il faut montrer que la droite de
Steiner (U'H) associée au point B' est orthogonale à la
droite (HE1) où
E1 est le point de
contact de la conique avec la droite (AC).
|
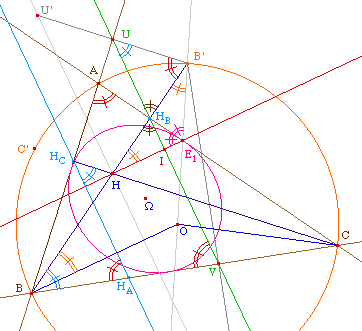
Les angles de marques de
même couleur sont de même
mesure
|
Première hypothèse
sur E1 : il est sur
la médiatrice de [HB']. On a donc les
égalités d'angles dans B'H E1 que
l'on voit sur la figure en B', H, et en
E1.
Seconde hypothèse sur
E1 : il est aussi
sur (OB'). OBB' est donc isocèle, avec les angles en
B et B' égaux. On remarquera par exemple que cela
signifie que (HE1) est parallèle à
(BO), mais cela ne sera pas utilisé par la suite.
Ainsi l'angle au centre B'OB est-il égal au double de
AE1B'.
Construction de
U : U, A, B' et HB
sont inscriptibles dans le cercle de diamètre
[AB'], donc les angles UB'H et BAC sont égaux
comme tous deux supplémentaires de UAC (ou
égaux dans le cas de l'hyperbole). Ainsi l'angle au
centre BOC est-il le double de UB'H.
Construction de
V : U, B, V, et B'sont
inscriptibles dans le cercle de diamètre
[BB'] et en particulier les angles B'UV et B'BV sont
égaux (ou supplémentaires dans le cas de
l'hyperbole). Ainsi l'angle au centre B'OC est-il le double
de l'angle B'UV.
Il résulte de ces derniers
résultats que la somme des trois angles HB'U, B'UV et
B'E1A est égale à un angle plat. Ce
qui est aussi le cas des angles HB'U, B'UV et
UHBB'. Cela sigifie que UHBB' et
B'E1HB sont égaux et donc que HI
HB est rectangle en I. Et donc que la droite de
Simpson (UV) de B' est orthogonale à
(HE1). C'est donc aussi le cas de la droite de
Steiner (U'H).
|
|

|
D'après le rappel
précédent, cette droite (U'H) coupe (AC) en un
point J de la directrice.
La droite de Steiner
associée au symétrique de l'orthocentre par
rapport à une droite support d'un côté
du triangle coupe cette droite en un point de la directrice
de la conique.
Remarques :
1 - Si le côté
(HAHC) est parallèle à
(AC), la droite de Steiner de B' est parallèle
à (AC), le point J n'existe pas : comme le triangle
est supposé non équilatéral, il existe
un côté du triangle orthique qui n'est pas
parallèle à son côté
associé, on peut alors toujours construire un point
de la directrice à partir de ce couple de
côtés.
2 - La preuve doit être
adaptée dans le cas de l'hyperbole. Il suffit de
reprendre les mêmes arguments et de les traduire par
exemple en angles de droites : d'une manière
générale, les angles égaux deviennent
éventuellement supplémentaires et
réciproquement : il est clair que l'argument en
angles de droites convient encore; l'argument de l'usage de
l'angle au centre double est d'ailleurs significatif
à ce sujet.
|
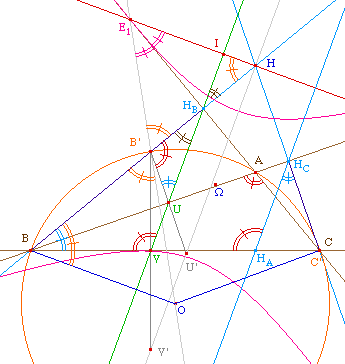
Cas de l'hyperbole : par rapport au cas
de l'ellipse,
ici UB'H et BAC sont égaux, alors que B'UV et B'BV sont
supplémentaires
On notera aussi que comme droite orthogonale de la droite des
centres des deux cercles, la directrice est parallèle à
l'axe radical des deux cercles. Il serait intéressant
d'observer le passage de l'un à l'autre.
Compléments sur la directrice
associée à H et l'axe radical des cercles
Comme dans la remarque ci-dessus, on supposera que ABC n'est
pas isocèle en B afin que les droites (AC) et
(HAHC)
ne soient pas parallèles. Soit K l'intersection de ces deux
droites.
|
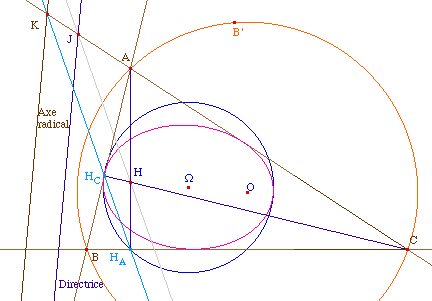
Illustration dans le
cas de l'ellipse
|
Les points AHCHAC sont
cocycliques, sur le cercle de diamètre [AC],
et donc les produits (algébriques) KA.KC et
KHC.KHA sont égaux, ce qui
signifie que K est sur l'axe radical des deux cercles
circonscrit et d'Euler du triangle ABC. Si le triangle n'est
pas isocèle (et pas rectangle), les trois
intersections des droites-côtés du triangle et
du triangle orthique se coupent en trois points
alignés qui sont sur l'axe radical de ces deux
cercles (qui s'appelle aussi l'axe orthique du triangle
ABC).
D'après ce qui précède, il est
alors immédiat que :
L'homothétie de centre C
qui transforme HC en H transforme K en J et donc
l'axe radical des deux cercles en la directrice de la
conique associée au foyer orthocentre.
On remarquera qu'il en serait de même de
l'homothétie de centre A transformant HA
en H.
|
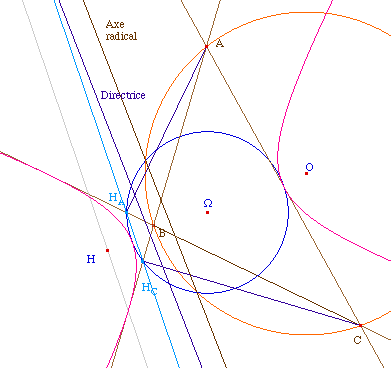
Illustration dans le cas de
l'hyperbole
On retrouve en particulier l'axe radical dans le cas où
les deux cercles sont sécants.
[2
- Conique définie par cercle principal et deux tangentes
]
[3 - Lieu du second foyer des
coniques connaissant un foyer, une tangente un point
]
[Retour Présentation
"Bifocale"] [Retour
Coniques] [Exercices
sur l'approche "bifocale"]
 Menu général
Menu général








