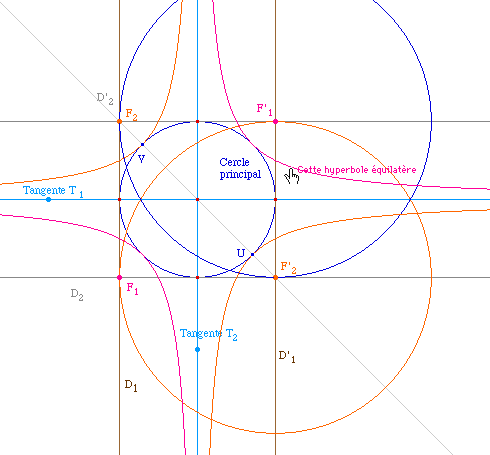
2 - Conique définie par cercle principal et deux tangentes
[1
- Cercle circonscrit et cercle
d'Euler]
[3 - Lieu du second foyer des
coniques connaissant un foyer, une tangente un point
]
[Retour Présentation
"Bifocale"] [Retour
Coniques] [Exercices
sur l'approche "bifocale"]
La projection orthogonale d'un foyer d'une conique à centre sur une tangente à cette conique appartient aussi à son cercle principal.
|
|
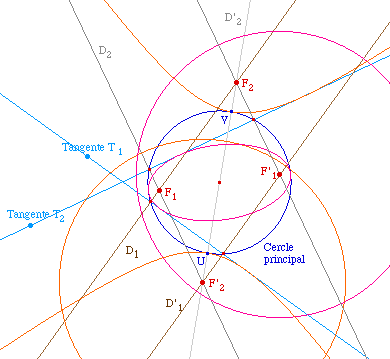
D'après le rappel, les deux tangentes T1 et T2 doivent couper le cercle principal. Notons D1 et D'1 les perpendiculaires à la droite T1 en ses points d'intersection avec le cercle. Les couples de foyers de la conique cherchée sont sur ces deux droites.Ils sont de même sur les droites D2 et D'2 orthogonales à T2 en ses points d'intersection avec le cercle principal. Les intersections des paires {D1, D2}, {D'1, D'2} donnent un premier couple (F1, F'1) de foyers solutions. Les intersections des paires {D1, D'2}, {D2, D'1} donnent un second couple (F2, F'2) de foyers solutions.
|
|
|
Si une des deux droites est aussi tangente au cercle (comme T1 ci-dessous), la macro précédente donnent deux coniques confondues, comme on le vérifie avec la gestion des ambiguïtés.
Les deux droites D1 et D'1 sont confondues à la perpendiculaire à T1 en le point de contact avec le cercle, c'est l'axe focal de la conique : il n'y a donc qu'un seule conique. De plus, l'autre droite T2, si elle n'est pas elle aussi tangente au cercle principal - et si elle n'est pas parallèle à T1 - a ses deux perpendiculaires associées D2 et D'2 qui coupent cet axe focal nécessairement à l'extérieur du cercle. Voir pourquoi ... c'est immédiat. Ainsi, la conique, quand elle n'est pas dégénérée (T1 et T2 parallèles), est donc toujours une hyperbole. |
|
|
Au contraire, si les deux droites T1 et T2 sont tangentes au cercle, la macro précédente donne deux coniques confondues avec le cercle, comme on le vérifie avec la gestion des ambiguïtés : on obtient alors nécessairement des ellipses ciculaires : D1 et D'1 sont confondues, de même pour D2 et D'2, et toutes les quatre passent par le centre du cercle; les foyers sont donc confondus. Cabri II recconnaît les ellipses circulaires. |