 |
|
[I. Introduction] [II. Les droites] [III. Cercles et distance] [V. Constructions] [VI. Exercices]
 |
|
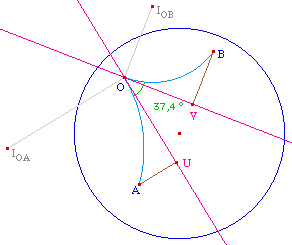
Remarque : la marque verte produite ne montre qu'un angle inférieur à 180°. Il serait plus long de faire plus général pour une utilisation assez marginale, et les macros étant déjà assez lourdes ...
|
|
|
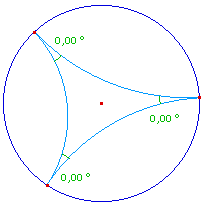
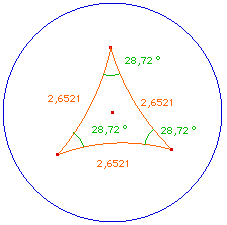
Triangle avec trois sommets
idéaux : |
 |
![]() HAngl06e.fig
(30 Ko)
HAngl06e.fig
(30 Ko)
|
|
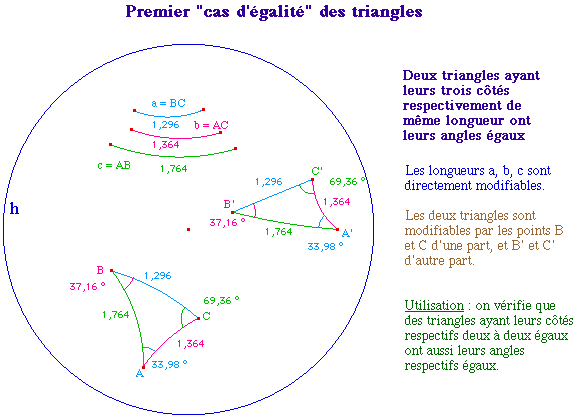
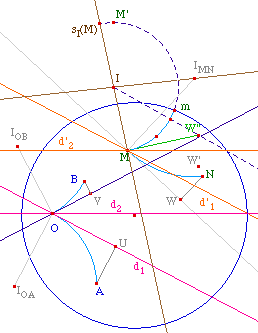
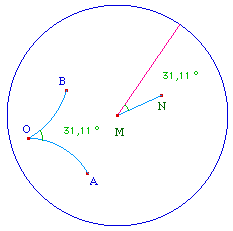
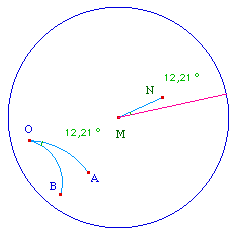
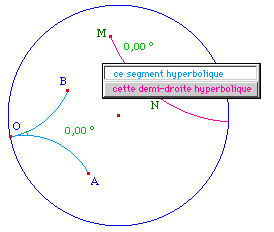
Il s'agit de reporter l'angle géométrique AOB sur la demi-droite [MX). On peut utiliser la même démarche métrique que dans le cas euclidien puisqu'en géométrie hyperbolique deux triangles de côtés de même mesure ont les mêmes angles. Le cercle de centre M et de rayon OA coupe [MX) en N. les cercles de centre M et N de rayons respectifs OB et AB se coupent en R et S.
Remarque : ce paragraphe est uniquement introductif au suivant, car la macro est inutilisable, elle prend environ 600 objets intermédiaires, et même en ne rendant qu'une seule demi-droite, on n'économise que 31 objets : il faut donc trouver autre chose ! (en fait, la macro Compas hyperbolique génère à elle seule 180 objets intermédiaires) |
|
|
 |
 |
 |
|

![]() HAngl07c.fig (PC) ou HAngl07M.fig
(Mac)
HAngl07c.fig (PC) ou HAngl07M.fig
(Mac)
![]() HAngl08c.fig
(50 Ko)
HAngl08c.fig
(50 Ko)
[I. Introduction] [II. Les droites] [III. Cercles et distance] [V. Constructions] [VI. Exercices]