 DrtHyp2.fig
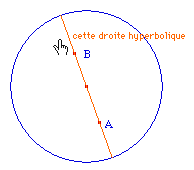
précisions sur la construction
DrtHyp2.fig
précisions sur la construction
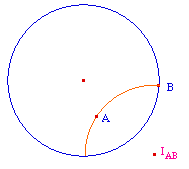
Important :
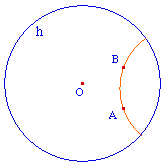
pour des utilisations ultérieures, on se
souviendra que le premier point
cliqué est un point constitutif de l'arc
"droite hyperbolique", mais pas l'autre.
|
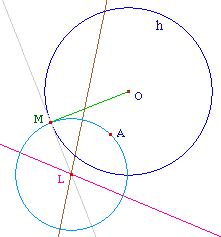
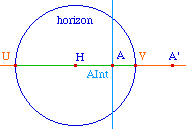
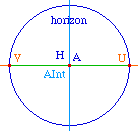
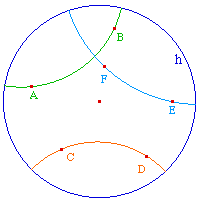
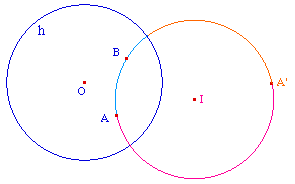
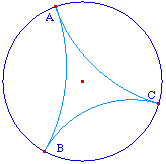
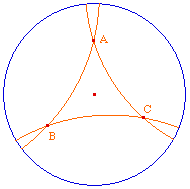
La droite hyperbolique (AB) est, sur cercle orthogonal
à l'horizon passant par A et B, l'arc inclus dans
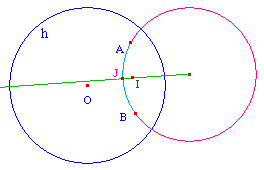
l'horizon (sans les extrémités). Dans le cas
où A et B sont alignés avec le centre de
l'horizon, c'est de diamètre euclidien passant par A
et B.
Il peut être utile, pour des constructions
annexes, d'avoir le centre. La macro
rend aussi le centre, que l'on peut cacher s'il ne sert
pas.
 DrtHyper.mac
DrtHyper.mac
Nom de la macro : Droite
hyperbolique
|
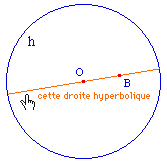
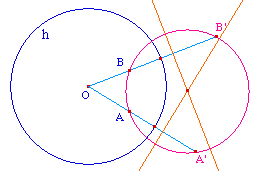
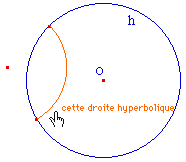
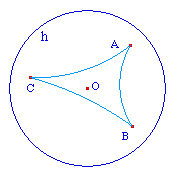
En redéfinissant le point A comme
étant le centre du cercle, on confirme la
robustesse de la macro ... et celle de Cabri par la
même occasion.
|