|
|
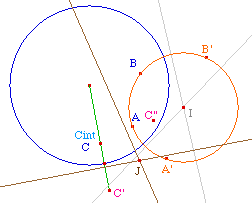
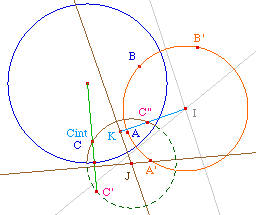
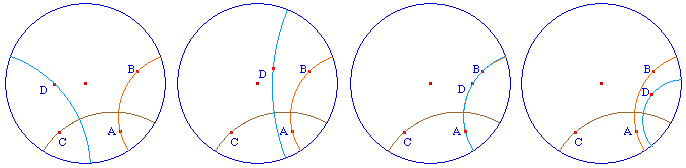
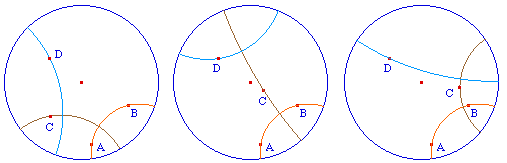
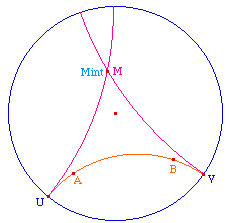
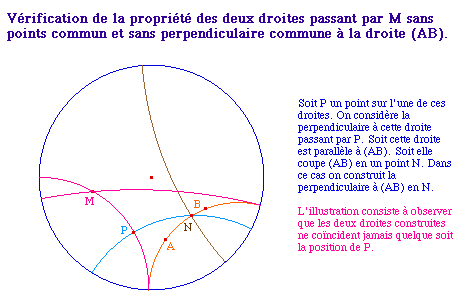
Etant donné un segment ou une droite hyperbolique [AB], ou (AB) et un point C, on veut construire la perpendiculaire à (AB) - ou [AB] - passant par C.Notons I le centre du cercle support, dans un premier temps inutile, car Cabri prend les inverses par rapport à un arc.Sous le point C, on construit Cint qui n'existe que si C est à l'intérieur du disque horizon, par la macro IntHoriz.mac.Notons C" l'inverse de Cint par rapport à (AB). Le centre de la perpendiculaire hyperbolique est donc sur la médiatrice de [CintC'] - car c'est une droite hyperbolique pour le disque h - et sur la médiatrice de [CintC"] car elle droit aussi être orthogonale à ce cercle. |