Tangente 2 - Tangentes parallèles à une direction donnée

Dans cette page nous utiliserons la propriété focale des tangentes : l'angle droit en F du triangle IMF où I est l'intersection de la tangente en M et de la directrice associée au foyer F.

Nous utiliserons aussi la construction point par point de la conique par l'intermédiaire d'un cercle associé dans le rapport e à la directrice.

La construction

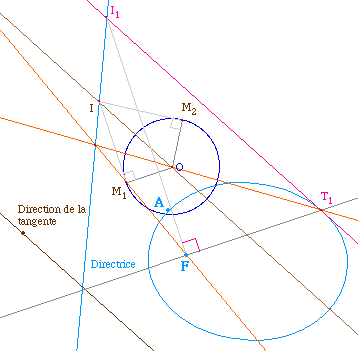
Dans la construction par cercle associé, le point T1 de la conique s'obtient par l'homothétique du segment [M1O] dans l'homothétie qui transforme M1 en F et dont le centre est sur la directrice. Puisque l'on sait que l'angle en F de T1FI1 doit être droit pour que (T1I1) soit la tangente en T1 à la conique, il suffit de trouver les points M du cercle associé qui satisfont à cette condition. L'homothétie réciproque (qui envoie T1en O) de cet angle droit est un angle droit. Si on veut que la tangente soit parallèle à une droite fixe, son image réciproque doit être la parallèle à cette droite passant par O. Soit I l'intersection de cette dernière avec la directrice. Les points M du cercle dont il faut construire les images sur la conique sont les points tel que IMO est rectangle en M. Ce sont donc les points de contact du cercle avec ses tangentes issues de I, notés M1 et M2 ci-dessus. Sur la figure, on a tracé le segment [FI1]. La marque de l'angle droit a été mise par Cabri. 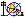TgtPara1.fig (figure partielle) ci-contre qui ne contient que le traitement du point M1.

Remarque : La présence de la conique sur cette figure est inutile pour la construction. Elle n'est là que pour vérifier de visu que l'on a bien construit une tangente à la conique définie par D, F et le point A. En particulier le point T₁ est obtenu comme intersection de deux droites et non pas d'une droite et de la conique comme on le ferait naturellement avec les nouveaux outils de Cabri II.

Le propos est bien ici d'illustrer que la construction d'une tangente parallèle à une direction donnée est réalisable à la régle et au compas à partir de la définition monofocale et d'elle seule.

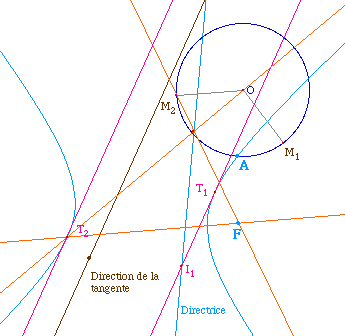
Voici la figure finale, dans le cas d'une hyperbole. Aspect technique : Pour avoir des "petites" figures dans les pages d'abraCAdaBRI, le cercle associé a été repris des pages précédentes où il est près de la conique car près de A. Pour une meilleure lisibilité, on peut le mettre plus haut. Pour cela, il suffit de redéfinir le point O ... qui doit resté un point construit, mais, en pratique, un peu plus loin de A. Figure finale TgtPara2.fig. La macro TgtePara1.mac associée. On remarquera qu'avoir pris deux points ayant des tangentes parallèles est une méthode (lourde) d'obtenir le centre d'une conique ... à centre. Justement, parlons-en ...

Et pour la parabole ?

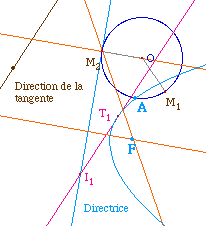
Il suffit de redéfinir F comme point sur objet du cercle de centre A tangent à la directrice pour voir ce qu'il se passe : un des deux points M1 ou M2 appartient à la directrice (indépendant du cercle associé retenu) et donc la tangente correspondante n'existe plus : Il n'y a qu'une tangente à une parabole parallèle à une droite donnée. En fait, en termes projectifs, l'autre est renvoyée à l'infini puisque le centre de la parabole aussi ... TgtPara3.fig spécifique à la parabole.

Menu général