|
|
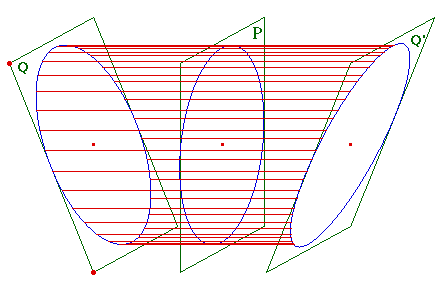
Supposons à présent que la direction de la
projection ne soit pas orthogonale, et plaçons nous
dans ce contexte de projection en vraie grandeur. Soit alors
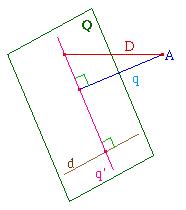
d la droite d'intersection des plans Q, Q' et P (voir
illustration ci-dessus)
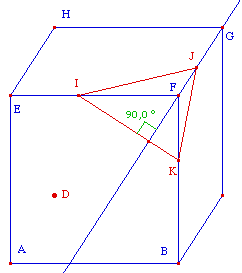
Les droites perpendiculaires au plan Q seront alors
projetées suivant des droites (puisqu'elles ne sont
pas parallèles à D), qui seront de plus
parallèles. Montrons que ces "fuyantes" sont
perpendiculaires à la droite d'intersection d des
plans Q, Q' et P. En effet, menons par un point A de la
droite D, une perpendiculaire q au plan Q. Le plan R,
défini par les droites D et q (sécantes en A),
coupe le plan Q suivant une droite q' qui n'est autre que le
projeté de la droite q.
Comme la droite d est orthogonale à la droite D
(car d est contenue dans P) et à la droite q (car d
est contenue dans Q), elle est par conséquent
orthogonale au plan R, donc à la droite q' qui est
contenue dan ce plan. Ce qu'il fallait prouver.
 ChVG02.fig
(ne sert que pour illustration ...)
ChVG02.fig
(ne sert que pour illustration ...)
|