Modèle
hyperbolique |
Modèle euclidien (parabolique) |
Modèle elliptique |
[2- Premières définitions
et axiomes] [3 - Lien avec les
modèles usuels] [4 -
Faisceaux et antiappariemment] [5 -
Faisceaux dans le triangle]
[6 - Axiomes introduisant les modèles
hyperboliques et elliptiques] [7 -
Axiomes des géométries affine et projective]
[8 - Tableau récapitulatif]
1 - L'évolution de la pensée vers la sortie d'une géométrie à caractère implicitement empiriste ("Histoire des GNE")
2 - L'effort réalisé à la fin du XIX° pour arriver à une axiomatique précise de la géométrie euclidienne ("Les fondements" de David Hilbert).
3 - Les différentes variantes autour des géométries construites selon les axiomes initiaux (les constructions de Cayley, les géométries non archimédienne ou non pyrthagoricienne ...)
4 - L'approche algébrique de la géométrie, et les liens entre les figures de base et le corps de nombres construit.
L'incidence sera interprétée en terme ensembliste : appartenance d'un point à une droite et inclusion d'une droite au plan. Intuitivement une droite peut être "parcourue" - peut-on se libérer du mouvement dans les interprétations ? - de deux façons, ce qui induit une relation d'ordre sur une droite. Une droite orientée est appelée un axe.
Un point d'une droite définit alors deux demi-droites. Deux points distincts A et B d'une droite définissent 4 demi-droites. On définit ainsi le segment [AB], les points du segment étant alors "entre A et B" pour les relations d'ordre sur la droite. Un segment orienté est appelé vecteur. Une demi-droite orientée est appelée rayon.
Le complémentaire d'une droite est formée de deux demi-plans (ouverts). Si deux points A et B sont dans l'un de ces demi plan, le segment [AB] ne rencontre pas la droite, alors que s'ils sont chacun dans l'un des deux demi-plans, le segment [AB] rencontre la droite.

Modèle
hyperbolique |

Modèle euclidien (parabolique) |

Modèle elliptique |
En parcourant un axe dans son sens croissant, on oriente le plan en décidant que que l'un des deux demi-plans (celui de gauche ou celui de droite) comme positif - respectivement négatif.On appelle drapeau, un triplet (A, d, p) où A est un point, d un axe incident à A, p un plan orienté incident à d.
Une réflexion de droite d est une bijection du plan qui transforme tout droite en une droite. La droite d est la seule qui soit invariante point par point. Si d et le plan sont orientés, par la réflexion d'axe d, la droite d conserve son orientation alors que le plan en change.
En composant les rélexions, on obtient les isométries du plan.
Deux drapeaux quelconques du plan sont l'image l'un de l'autre par une isométrie (on sait que trois réflexions suffisent).Les droites conservées (globalement) par la réflexion de droite d, différentes de d, sont dites orthogonales à d. Alors d est aussi orthogonale à ces droites.
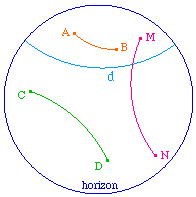
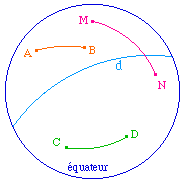
Exemple de la représentation hyperbolique du cercle de Poincaré :
Le plan est l'intérieur d'un cercle, appelé horizon
les points sont les points à l'intérieur de l'horizon,
les droites sont les traces dans l'horizon des cercles orthogonaux à l'horizon,
La symétrie orthogonale est l'inversion euclidienne par rapport au cercle support de la droite.
Alors, si on sait que l'inverse d'un cercle orthogonal au cercle d'inversion est globalement invariant (par conservation des tangentes par exemple) il est facile de vérifier que dans cette interprétation, la symétrie orthogonale par rapport à une droite d :
a) est une bijection du plan qui envoie un demi-plan sur l'autre et laisse la droite invariante point par point.
b) l'image d'une droite est une droite.
c) les seules droites globalement invariantes ont pour support un cercle orthogonal à la fois à l'horizon et à la droite d.C'est exactement ce modèle que l'on "redécouvrira" au cours de la présentation de la géométrie hyperbolique.
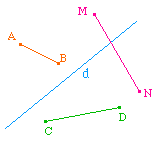
Ci contre on observe clairement que (AA'), (BB') et (CC') sont orthogonaux à d qui est leur perpendiculaire commune.
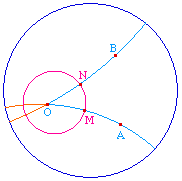
Dans un plan orienté, on appelle angle orienté un couple - ordonné - de demi-droite (les deux côtés de l'angle) de même origine (le sommet). Pour définir des opérations sur les angles - comparaison ou addition - et les mesurer, on est amené à considérer leur intersections avec le cercle de centre le sommet de rayon 1 - ici on suppose que la géométrie est assez riche pour qu'un tel cercle existe et que les intersections avec les demi-droites existent.
 |
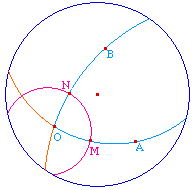 |
Les droites support des demi-droites sont orientées dans le sens naturel de la demi-droite : de l'origine O à un point de la demi-droite (A ou B ci-dessus). L'arc orienté associé à un angle orienté - ci-dessus l'angle (OA, OB) - est celui contruit depuis la première demi-droite à la seconde en restant à la fois dans le demi-plan positif par rapport à la première demi-droite et dans le demi-plan négatif par rapport à la seconde.
Pour comparer ou additionner des angles orientés, on définit ces opérations à partir de classes d'équivalences : deux angles sont dans une même classe si l'on peut passer de l'un à l'autre par un nombre pair de symétries (isométrie directe). Les additions des classes d'équivalence se font en prenant deux représentants de même sommet tel que le second côté du premier angle coïncide avec le premier côté du second angle. Le résultat est indépendant du choix des représentants. Toutefois, pour avoir une relation d'ordre compatible avec l'addition il faut quotienter par 2PiZ ...