[III.1. Approche expérimentale du cercle] [III.2 - Construction du cercle] [III.3 Médiatrice, milieu ...] [III.5 - Tangentes] [III.6 - Premières utilisations]
[I. Introduction] [II. Les droites] [IV. Les angles] [V. Constructions] [VI. Exercices]
[Retour aux GNE] [Menu général]
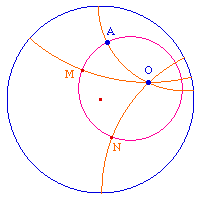 |
Considérons un cercle hyperbolique de centre O passant par A. Alors toutes les droites hyperboliques passant par O sont aussi orthogonales à ce cercle. Cela serait facile à montrer avec notre construction (à considérer comme un exercice sur l'inversion). Cette propriété pourait d'ailleurs être une autre approche pour la construction des cercles : elle est proposé dans [Berger].Autrement dit les traces des droites hyperboliques du disque de Poincaré passant par le centre d'un cercle hyperbolique sont des droites hyperboliques pour le disque de Poincaré associé à ce cercle.Rappelons que le centre hyperbolique d'un cercle, son centre euclidien et le centre de l'horizon sont alignés. |
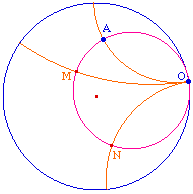 |
On s'intéresse maintenant à ce que devient ce cercle - ou ces droites - quand le centre O tend vers l'infini, c'est-à-dire se rapproche du cercle horizon. On voit que la droite (OA), ainsi que toutes les droites comme (OM) et (ON) de l'illustration sont toujours orthogonales au cercle limite et ont le point limite comme point infini sur le cercle.Ainsi, si O est un point (à distance infinie) de l'horizon - point idéal - cette courbe est orthogonale à toute droite ayant ce point O comme point infini. Ce cercle s'interprète donc comme un cercle dont le centre est à l'infini. Et contrairement au contexte euclidien, cette courbe n'est pas une droite hyperbolique. Comme ce n'est pas non plus un cercle puisque son centre n'est pas un point du plan hyperbolique, on lui donne un nom : c'est un horocycle.Remarque : [Berger] l'appelle horicycle. |
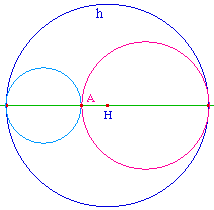 |
Un horocycle est traditionnellement défini par le point diamétralement opposé à son point à l'infini. Pour un point A autre que le centre de l'horizon, il y a deux horocycles. Ici pour la construction, on peut prendre aussi bien la droite (AH) que la droite (AA') - avec A' inverse de A par rapport à l'horizon - car l'horocycle passant par le centre H n'est pas défini : il y en a une infinité.
|
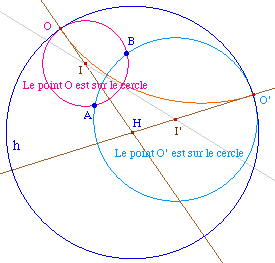 |
Soient A et B deux points. Un horocycle a son centre hyperbolique O sur le cercle horizon. Il est a distance infini de A et de B. Mais, comme centre d'un cercle, il est aussi à même distance de A et de B. Ainsi, le point infini de l'horocycle n'est autre que l'un des points infini - sur le cercle horizon - de la médiatrice hyperbolique de A et B. Soient O et O' ces deux points. Les centres euclidiens des deux horocycles - notons les I et I' - sont sur les droites (OH) et (O'H). Puisque les horocycles sont des cercles euclidiens, ils sont aussi sur la médiatrice euclidienne de [AB]. Ce qui permet la construction de I et I'.Construisons les cercles de centre I et I' passant par A. Avec Cabri testons l'appartenance de O et O' à ces deux cercles. La confirmation de Cabri illustre la cohérence de cette construction avec celles antérieures.On laissera en exercice une preuve - par des arguments sur les inversions - que par construction de O, I est aussi sur la médiatrice euclidienne de [AO].
|
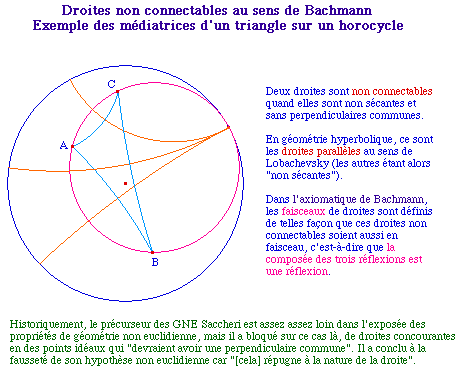
Voir l'extrait de présentation historique consacré à Saccheri.
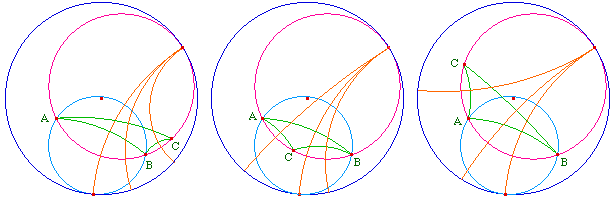
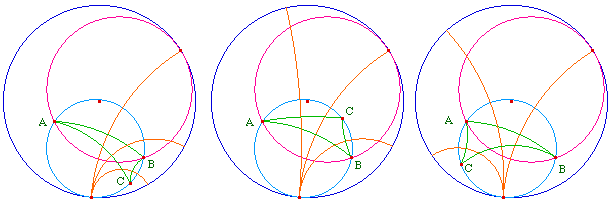
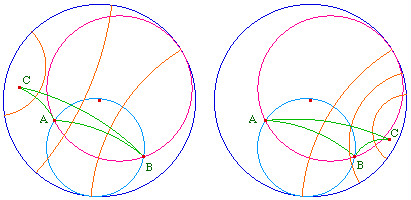
L'extérieur ne convient pas
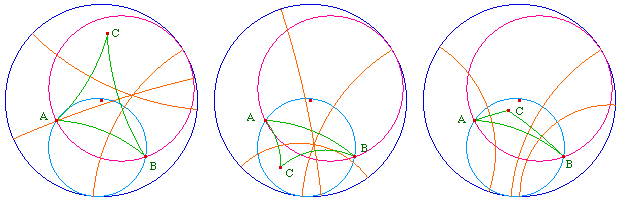
L'intérieur convient, sauf la partie commune aux deux horocycles
Etant donnés deux points A et B. Le lieu du point C pour lequel le triangle ABC a ses médiatrices concourantes - ie pour lequel A, B et C sont hyperboliquement cocycliques - est la différence symétrique des intérieurs des deux horocycles passant par A et B.
[III.1. Approche expérimentale du cercle] [III.2 - Construction du cercle] [III.3 Médiatrice, milieu ...] [III.5 - Tangentes] [III.6 - Premières utilisations]
[I. Introduction] [II. Les droites] [IV. Les angles] [V. Constructions] [VI. Exercices]