Modèle hyperbolique de Klein
- Beltrami
KB.1.a - Présentation
générale du dossier - Premières macros
métriques
[Introduction] [Orthogonalité
et symétries] [Cercles et
horocycles] [Angles]
[Coniques]
[Retour aux GNE]
[Le modèle de
Poincaré] [Historique
des GNE]
Contenu | Droites du modèle |
Macros métriques | Barre
de menu
Sur le contenu et l'organisation du
dossier
Certaines figures du modèle de Klein Beltrami (KB) vont
être plus faciles à réaliser que dans le
modèle du disque de Poincaré - en terme d'objets Cabri
à construire - puisque les droites sont des segments de
droites euclidiennes. Il en résulte en particulier qu'il n'y a
aura pas de gestion particulière à effectuer pour le
fonctionnement sur les points idéaux (points du cercle
horizon).
D'autres figures seront plus longues puisque les cercles
hyperboliques sont des coniques euclidiennes par exemple. Mais d'une
manière générale les figures sont moins lourdes
que dans le modèle de Poincaré. De même, dans un
soucis d'allègement, dans ce dossier, contrairement à
celui traitant du modèle de Poincaré, on a
renoncé à gérer la position des points à
l'intérieur de l'horizon, cela alourdissait inutilement
certaines figures, par application de macros successives.
Ce dossier se veut d'une lecture plus rapide que celui sur le
modèle de Poincaré (supposé avoir
été parcouru - par exemple dans
sa version CabriJava suffisamment condensée : cela
évitera quelques redites). Pour l'efficacité des
figures, on choisira parfois l'argumentation métrique pure -
usage direct de la distance - alors que pour d'autres, on choisira
l'approche géométrique, les constructions de ce
modèle étant alors entièrement basée sur
la division harmonique et l'homologie harmonique. Toutes les figures
- y compris aux cas limites - sont réalisables
entièrement géométriquement, mais pour un gain
d'objet - en particulier dans les macros - il est parfois judicieux
d'utiliser d'autres arguments.
Que ceux des lecteurs pour lesquels le terme "homologie" fait
froncer les sourcils se rassurent : leur présence dans ce
dossier est uniquement constructive, il n'y a aucune
difficulté théorique soulevée ici, on n'utilise
que la notion de pôle d'une droite et de polaire d'un point par
rapport à un cercle, et tout ceci est rappelé en
détail dans une page de présentation (KB.1.b)
des "macros projectives utilisées". Il est d'ailleurs assez
fascinant de réaliser, pour l'occasion, une macro division
harmonique dans laquelle 3 des 4 points de la division peuvent aller
à l'infini.
Contenu | Droites
du modèle | Macros métriques |
Barre de menu
Les droites dans le modèle de Klein
Beltrami
|
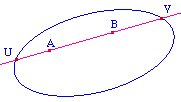
Historiquement, Cayley a d'abord montré que
l'intérieur d'une conique - projective réelle
-non dégénérée, munie de la
distance
d(A,B) = k.|
ln[(AU/AV)/(BU/BV)] |
est un modèle de géométrie
hyperbolique dans lequel la droite (AB) est l'intersection
de la droite euclidienne avec l'intérieur stricte de
la conique.
Cette page utilise
la distance de Cayley
|
Le rapport dans le logarithme est le birapport des 4 points,
noté [A, B, U, V]. Comme les transformations qui
conservent le birapport - donc les isométries du modèle
- sont de nature projective, il est clair que la notion d'homologie
sera - selon le point de vue - sous-jacente ou omniprésente.
D'autre part comme on travaille sur un cercle, l'homologie harmonique
sera suffisante, c'est-à-dire la transformation
associée à la division harmonique.
A l'occasion de travaux (rapidement
rappelés ici), Beltrami, en 1868, retrouve la
métrique de Cayley dans le cas où la conique est un
cercle, et étudie le premier modèle - car c'en est un -
de géométrie hyperbolique plane. Ce modèle a
l'inconvénient d'être non conforme, ce qui fait que les
constructions - pour l'orthogonalité et les angles en
particulier - ne sont pas aussi "euclidiennes" que dans les
modèles conformes ultérieurs de Poincaré.
|
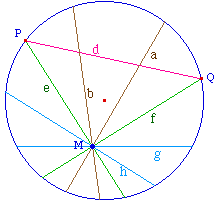
Le plan hyperbolique est
l'intérieur strict d'un
disque dans lequel les droites sont les
sécantes du disque (ci-contre P et Q sont des points
idéaux, ils
n'appartiennent pas à la droite d). Dans un plan
hyperbolique il existe au moins deux droites
non connectables (ie sans point
commun et sans perpendiculaires communes). De plus, pour
tout point A n'appartenant pas à une droite d, il
existe au moins une droite passant par A non connectable
à d. En pratique il en existe toujours deux.
La distance de A et B est d(A,B) =
|ln[(AU/AV)/(BU/BV)]|, comme ci-dessus.
Ci-contre, parmi les droites du faisceau issu de M, on
distingue
Les droites
sécantes à d
(exemple a et b).
Les droites non connectables
à d (ex. e et f), celles que Lobachevsky appelle
parallèles
Les droites non
sécantes à d : elles sont
connectables sans point commun, et donc ont une
perpendiculaire commune avec d (exemple g et h).
|
L'orthogonalité et la
symétrie orthogonale sont
directement liées, respectivement, au pôle d'une droite,
et à l'homologie harmonique qui, quand son centre est le
pôle de son axe par rapport à un cercle, laisse ce
cercle - et son intérieur - globalement invariant, tout comme
l'inversion par rapport à des cercles orthogonaux que sont les
symétries orthogonales dans le modèle de
Poincaré.
|
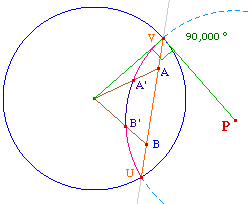
On notera que géométriquement,
deux points fondamentaux sont
communs aux deux modèles : le centre du
cercle orthogonal à l'horizon passant par la droite
hyperbolique de points idéaux U et V dans le
modèle de Poincaré
est le pôle de
cette même droite idéale (UV) dans le
modèle de Beltrami.
Ainsi d'éventuelles
propriétés sur les pôles de segments
dans les figures du modèle de Klein-Beltrami seront
donc aussitôt transférables en
propriétés sur les centres des segments
hyperboliques correspondants dans le modèle de
Poincaré. Nous y reviendrons, sur
les polygones réguliers par
exemple, lors des pages sur le cercle.
Cette simple remarque aide à mieux percevoir le
passage d'un modèle à l'autre, et permet
même de réaliser, par conjugaison, des
constructions dans un modèle en utilisant leur
homologue dans l'autre modèle. Le détail du
passage effectif de [AB] dans le modèle de
Beltrami à [A'B'] dans celui de
Poincaré est proposé dans Passage
d'un modèle à l'autre de l'introduction
générale aux constructions hyperboliques.
|
Contenu | Droites
du modèle | Macros métriques | Barre
de menu
Premières macros : distance et
milieu
Aprés deux macros cosmétiques comme  DroiteKB.mac ou DDrteKB.mac
(demi-droite), on peut aborder les macros de calcul et une
première construction :
DroiteKB.mac ou DDrteKB.mac
(demi-droite), on peut aborder les macros de calcul et une
première construction :
 DistKB.mac et MilieuKB.mac
DistKB.mac et MilieuKB.mac

 MilieuKB.fig ou MilieuKB.mac
MilieuKB.fig ou MilieuKB.mac
La construction du milieu a été faite par
intersection de ligne de niveau IU/IV = "constante connue" avec la
droite (AB). Cette construction a été faite avec la
calculatrice Cabri pour économiser les objets. Elle est
toutefois entièrement constructible
à la règle et au compas car
l'égalité abs(ln(p)) = abs(ln(q)) entraine p = q ou p =
1/q ce qui correspond à deux point symétriques par
rapport à une origine sur une droite. On peut donc, comme dans
la figure ci-dessus, chercher le point qui correspond à
l'égalité sur la demi droite [AB) : ce sera le
milieu. À partir de d(A, I) = d(A, B)/2, on voit donc
apparaître une racine carrée, et la relation pour le
point I comme écrit dans la figure.
Contenu | Droites
du modèle | Macros métriques
| Barre de menu
Pour les plus pressés : barre de
menu "modèle de Klein-Beltrami"
 BarreKB.men
(78 Ko) - Barre du 24 novembre
99
BarreKB.men
(78 Ko) - Barre du 24 novembre
99
Remarque : le
webmestre d'abraCAdaBRI n'est pas particulièrement
doué pour les icones, si une personne veut proposer un jeu
d'icones pour cette barre, elle sera la bienvenue ;-)
[Introduction] [Orthogonalité
et symétries] [Cercles et
horocycles] [Angles]
[Coniques]
[Retour aux GNE]
[Le modèle de
Poincaré] [Historique
des GNE]
 Menu général
Menu général



