[Retour aux GNE] [Le modèle de Poincaré] [Historique des GNE]


 |
 |
|
|
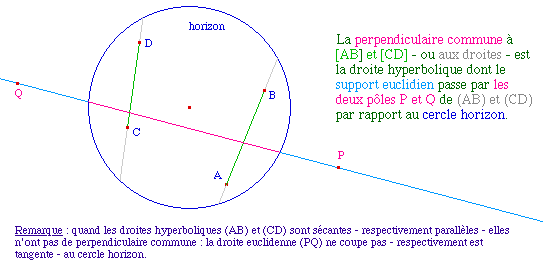
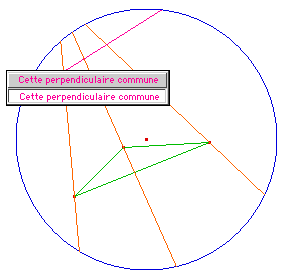
On a dit, dans la présentation des macros projectives pour le modèle hyperbolique, que la médiatrice de deux points A et B est l'axe d'homologie échangent A en B qui laisse le cercle horizon invariant.
Ci-contre on vérifie que ses points sont équidistants de A et B. Avec les macros précédentes, on pourrait aussi vérifier que la médiatrice est bien la perpendiculaire à [AB] en son milieu. |
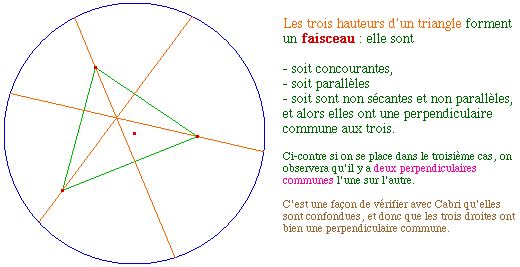
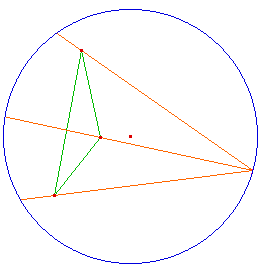
Les médiatrices d'un triangle forment aussi un faisceau
 |
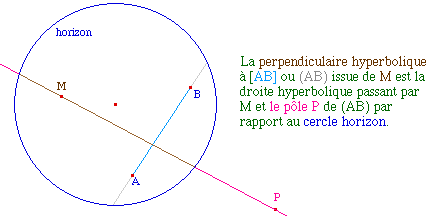
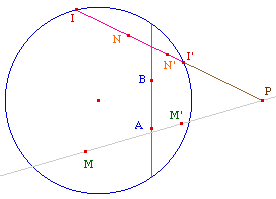
C'est simplement une utilisation de la macro homologie harmonique : à partir du segment [AB], on construit la droite (AB), son pôle P par rapport au cercle. M' est l'homologue harmonique de M dans l'homologie d'axe (AB) et de centre P. Tout a été fait, dans la macro division harmonique, pour que cette figure fonctionne dans tous les cas limites. |
|
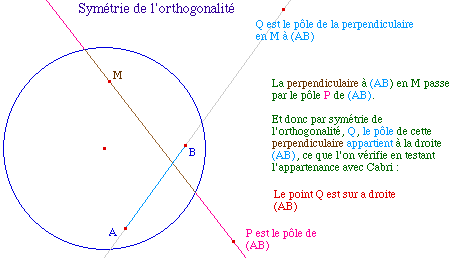
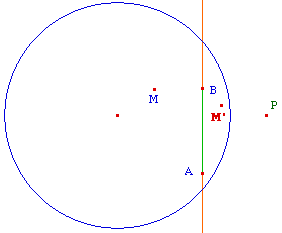
Premières propriétés de la symétrie orthogonale Il est facile de vérifier expérimentalement les propriétés de base de cette symétrie qui en fait la transformation première de cette géométrie. On peut vérifier qu'elle respecte la définition des réflexions de l'axiomatique de Bachmann : - La symétrie orthogonale transforme les droites en droites,échange les demi-plans hyperboliques créés par son axe. Ces propriétés résultent immédiatement de propriétés de l'homologie harmonique rappelées dans la page de présentation des "macros projectives" et en particulier du fait que le centre de l'homologie est le ^pole de son axe par rapport au cercle. |
L'homologie harmonique comme symétrie orthogonale et l'axiomatique de Bachmann
Dans cette axiomatique - comme dans d'autres - le concept de réflexions et d'isométries remplace la congruence des axiomatiques de type Euclide-Hilbert : le groupe des isométries permettra d'écrire plus simplement - avec le vocabulaire de l'algèbre - certaines propriétés géométriques de base.
Le groupe d'axiomes "M3" sur les réflexions dans l'axiomatique de Bachmann est le suivant :
Toute droite d est l'axe d'au moins une réflexion
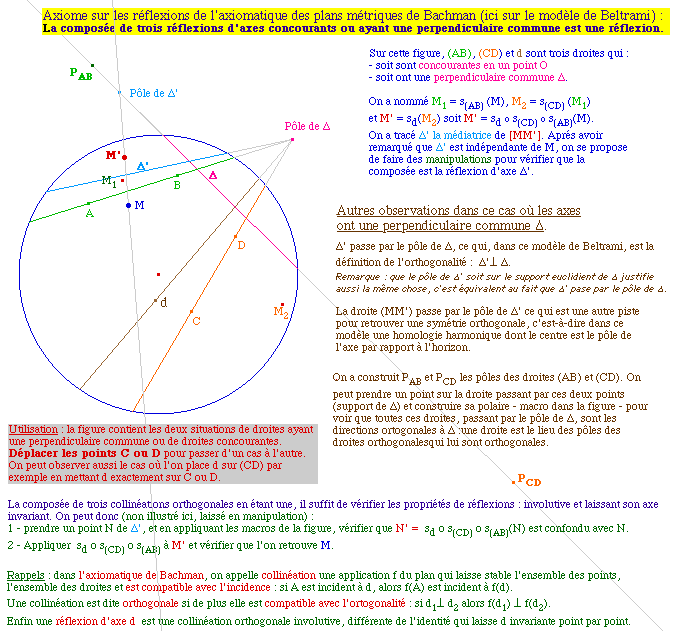
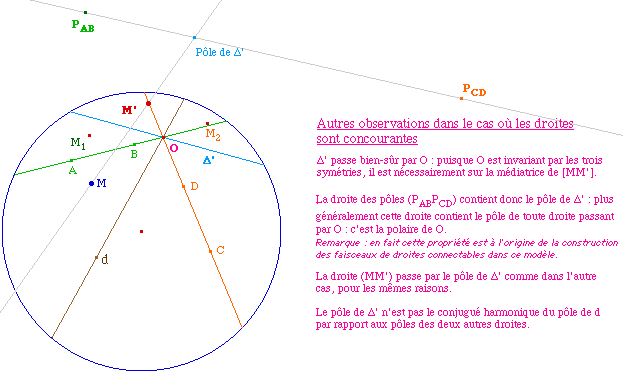
La composée de trois réflexions par rapport à trois droites ayant en commun un point ou une perpendiculaire est une réflexion par rapport à une droite.Voici deux illustrations, réalisées sur la même figure par des considérations de géométrie logique, qui résument la situation.
La symétrie centrale
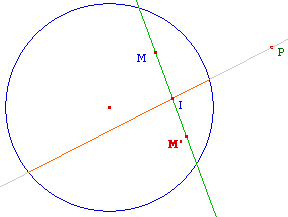 |
On utilise la figure sur la symétrie orthogonale : pour M différent de I, on peut tracer la droite (MI), son pôle P par rapport au cercle. Alors le symétrique de M par rapport à I est le symétrique orthogonal de M par rapport à la droite hyperbolique supportée par (PI).
|
Toutefois, on notera que cette construction est assez lourde (M' est le 46 ième objet de la macro). On peut économiser 10 objets en ayant une approche plus analytique, sur la base de la relation de la distance, comme pour la construction du milieu déjà vue précédemment :
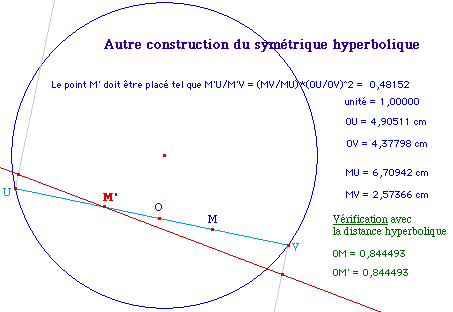
[Retour aux GNE] [Le modèle de Poincaré] [Historique des GNE]