|
|
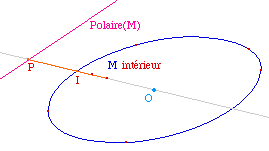
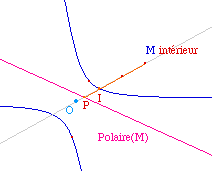
Tout d'abord - cela a
déjà été utilisé dans les
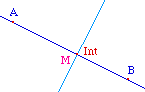
page d'introduction - le quadrilatère est convexe ssi
l'intersection I de ses diagonales existe. On construit donc
un premier point M' sous M qui n'existe que si I existe
(symétrique de I par rapport au milieu de I et
M).
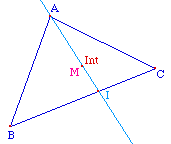
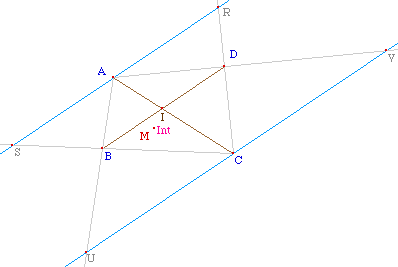
On trace ensuite les
parallèles à [BD] passant par A et C,
puis les quatre demi-droites [AD), [AB), [CD) et
[CB). Les deux premières coupe la droite passant
par C en U et V, les deux autres la droite passant par A en
S et R. Il est alors clair que M' est à
l'intérieur du quadrilatère ABCD si et
seulement si il est à la fois dans les triangles AUV
et CRS.
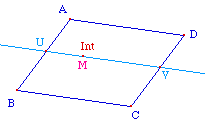
On utilise donc, une
première fois, la macro
Intérieur
Triangle pour construire sous
M' un point M" qui n'existe que si M' est à
l'intérieur de AUV. Puis on l'utilise une seconde
fois pour construire le point Int, sous M" si M" est
à l'intérieur de CRS.
|