|
|
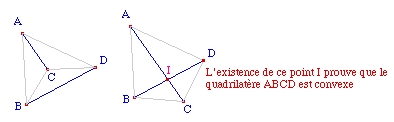
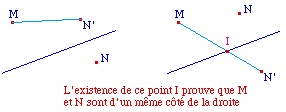
Soit M un point intérieur
à un triangle ABC. On aimerait construire un point
Int
qui n'existe que si M est à l'intérieur du
triangle. On peut donc penser utiliser 3 fois le
raisonnement précédent : M est à
l'intérieur du triangle si M et A sont du même
côté de (BC)
ET, M et B du même
côté de (AC)
ET
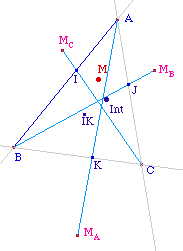
M et C du même côté de (AB). On construit
ainsi les trois points I, J et K sur les droites contenant
les côtés du triangle.
M est donc à
l'intérieur si et seulement si ces trois points
existent simultanément. On peut rendre compte de cet
état en
remplaçant le ET précédent par un
milieu : le milieu de deux
points n'existe que si ces deux points existent
simultanément. On peut donc prendre le milieu IK de I
et K. Le point
Int,
comme milieu de IK et J convient puisqu'il n'existe que si
les trois points existent simultanément, c'est
à dire si M est bien, à la fois, dans les
trois demi-plans qu'il convient.
 IntTR.fig
pour visualiser les différents comportements des
points MA, MB, MC et du
point
Int.
IntTR.fig
pour visualiser les différents comportements des
points MA, MB, MC et du
point
Int.
Rappelons toutefois que cette
approche n'est pas du tout optimisée. Elle a
seulement servi ici à mettre en évidence
qu'un ET logique se construit
facilement dans Cabri, par
milieu ou, si ce sont des objets, par
intersection.
|