[Introduction] [Orthogonalité et symétries] [Cercles et horocycles] [Angles] [Coniques]
[Retour aux GNE] [Cercles dans le modèle de Poincaré] [Historique des GNE]
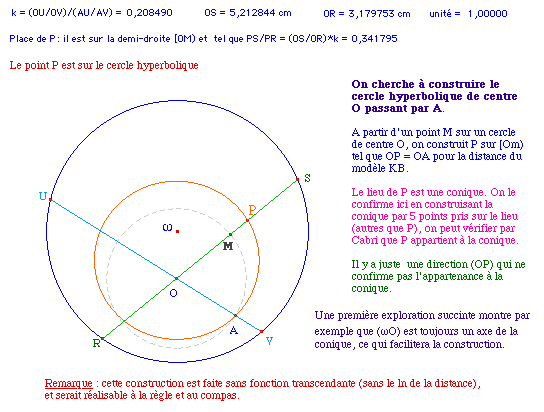
Une construction purement géométrique du cercle hyperbolique de centre O passant par A a donné lieu à une macro qui réalise la construction en 136 objets intermédiaires. On veut améliorer ce résultat par une autre approche.
Nous avons déjà vu (en KB.1.a) que si abs(ln(p)) = abs(ln(q)), alors soit p = q, soir p = 1/q. Pour avoir une approche du cercle hyperbolique de centre O passant par A, nous allons, à partir d'un cercle euclidien de centre O passant par A et d'un point M sur ce cercle, construire le point P sur la demi-droite [OM) dans le "cas p = q". On voit bien que l'autre cas "p = 1/q" correspondrait au symétrique hyperbolique de ce point. Comme M va décrire le cercle euclidien, on peut se limiter à la solution sur la demi-droite.

Sur l'illustration nous avons caché le lieu de P que l'on peut faire apparaître en chargeant la figure. Sans référence à l'homologie, comme utilisé à la page précédente, une preuve analytique du résultat ne pose pas de problème particulier.
Pour divers explorations sur ce lieu - dans le cas d'une exploration sans référence à l'homologie par exemple - on peut utiliser les macros relatives aux coniques, et plus spécifiquement aux ellipses, comme :
AxesHE.mac, ConikCtr.mac, Foy2Mac.fig construites dans ce dossier (ci dessous, seule la première est utilisée)
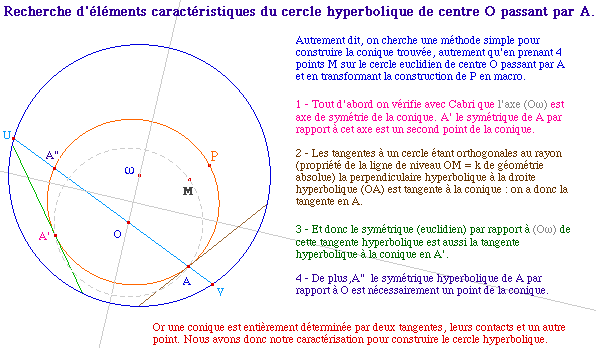
La construction d'une conique connaissant deux tangentes, leurs
contacts et un troisième point est une application des cas
particuliers du théorème de Pascal sur les coniques. On
utilisera donc cette macro ![]() Cnk1P2TC.mac
construite à cette
page du dossier sur les coniques affines.
Cnk1P2TC.mac
construite à cette
page du dossier sur les coniques affines.
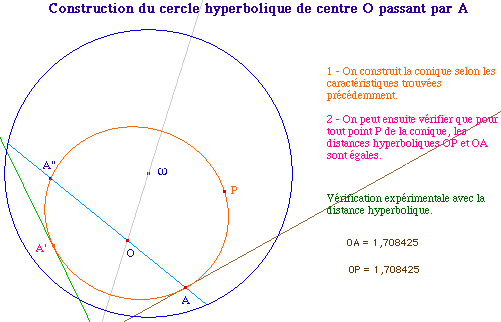
Remarque : la construction précédente fonctionne si O est un point idéal de l'horizon, et donc cette macro renvoie aussi l'horocycle de centre O passant par A.
Dans la macro associée, le cercle hyperbolique est le 78° objet. C'est mieux que les 136 de la construction géométrique, mais reste un peu lourd pour un cercle. Nous nous proposons donc de chercher à économiser les objets.
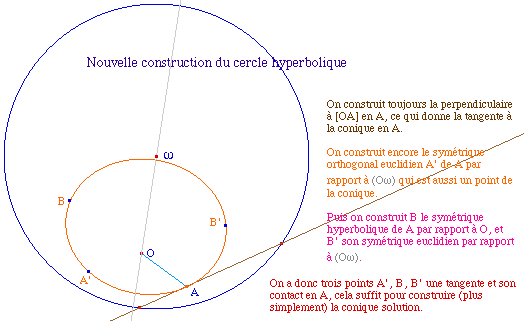
Pour cela, on peut remarquer que la macro utilisée sur les
coniques utilise elle-même une macro de construction ![]() Cnk3P1TC.mac
connaissant 3 points, une tangente et son contact construite à
cette
page. Or il est facile d'utiliser cette caractérisation,
et nous allons "économiser" 15 objets : la conique sera le
63° objet.
Cnk3P1TC.mac
connaissant 3 points, une tangente et son contact construite à
cette
page. Or il est facile d'utiliser cette caractérisation,
et nous allons "économiser" 15 objets : la conique sera le
63° objet.
Remarque : les deux macros fonctionnent au centre de l'horizon si on fait glisser le centre O sur ce point (mais pas si on y applique la macro. Par contre la seconde macro ne s'applique pas si O est pris comme point idéal.
On observera sur ces figures que les centres centrés au centre de l'horizon sont des cercles euclidiens - ce qui a été la base de notre construction géométrique - que le cercle de centre O passant par A idéal est un cercle idéal : c'est l'horizon lui-même.
3.a Construction "géométrique" | 3.b Construction "métrique" | 3.c Les horocycles | 3.d Premières utilisations
[Introduction] [Orthogonalité et symétries] [Cercles et horocycles] [Angles] [Coniques]
[Retour aux GNE] [Cercles dans le modèle de Poincaré] [Historique des GNE]