|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 - Première extension
27 triangles équilatéraux pour 27 points
particuliers
[1 -
Théorème initial] [2
- Les 6 trissectrices d'un angle - Notations]
[4 - Autres triangles
équilatéraux de la configuration ]
[5 - Commentaires et figures
finales] [6 -
Compléments]
[7 - Historique et
Références] [Retour
"Grands Classiques"] [Retour
"Géométrie Plane"]
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
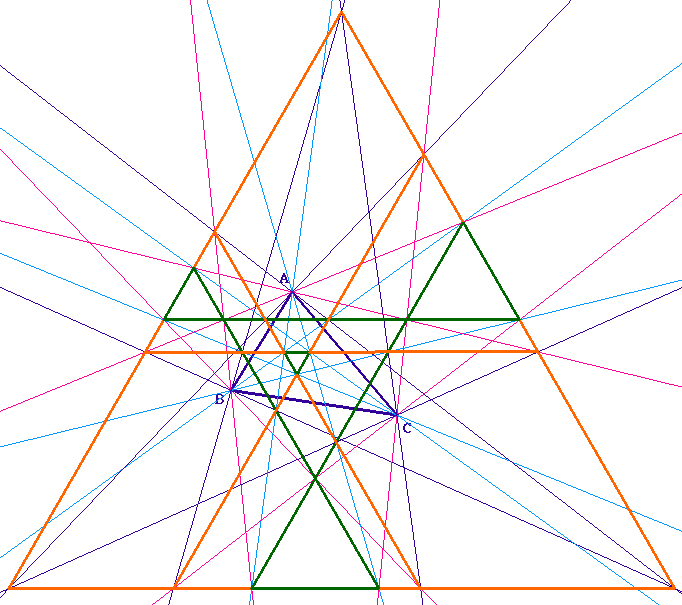

![]() Morley02.fig (figure
intermédiaire)
Morley02.fig (figure
intermédiaire)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
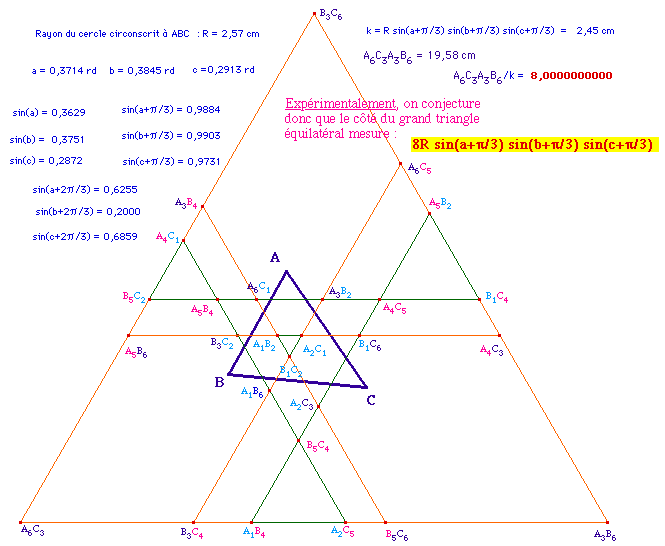
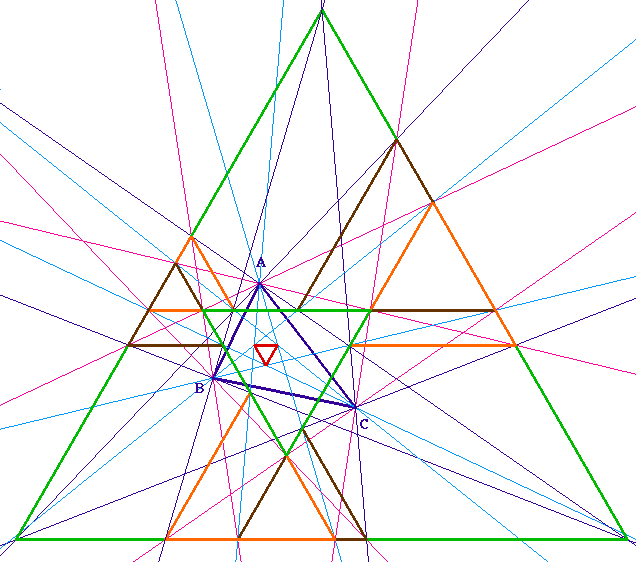
![]() Morley03.fig (figure
intermédiaire)
Morley03.fig (figure
intermédiaire)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|