Utilisation de l'outil "Puissance"
4 - Un problème d'Apollonius : Cercles tangents à 3 cercles

 [U1 - cercles tangents à une droite et passant par 2 points] [U2 - cercles tangents à un cercle et passant par 2 points
[U3 - cercles tangents à deux cercles et passant par un point]

[Résultats généraux] [Axe radical] [Théorème de Pascal]
[Exercices sur la puissance et les axes radicaux] [Retour Géométrie 2D]

 

Etant donnés trois cercles (de rayons distincts), on se propose de construire les cercles tangents à ces trois cercles, toujours sans utilisation de l'inversion, mais en respectant les capacités dynamiques de Cabri. Il y a, au maximum, 8 solutions possibles.

 

Pour faire les figures, quelques macros sont nécessaires (dont deux propres à cette page) :

Charger les macros Compar3C.mac qui est une macro d'Alice, et les macros construites pour cette page V2C1PmT.mac et V2C1PpmT.mac.

Compar3C.mac : renvoie sur 3 cercles, des cercles ordonnés (le plus petit ...)

V2C1PmT.mac : renvoie les cercles tangents à 2 cercles donnés passant par un point donnés et qui ont le même type (mT) de contact avec les cercles de base : deux contacts extérieurs ou deux intérieurs. La macro renvoie les points de contact sur le second cercle cliqué.

V2C1PpmT.mac: comme le précédent, mais ne renvoie que les cercles de contacts différents (pas même type - pmT) : il y a donc un contact intérieur et un extérieur.

Remarques : la macro sur les cercles tangents extérieurement utilise les centres d'homothétie, donc la construction que l'on va réaliser ne fonctionnera pas quand deux au moins des trois cercles auront exactement le même rayon. Ce sera la seule restriction à l'utilisation de la figure que l'on va construire ... (à améliorer toutefois donc ...)

Les deux macros précédentes ont été construites pour cette page (d'où le préfixe V pour Viète), sur la base des figures équivalentes de la partie Puissance du site.

 

Le principe de Viète.

C'est simplement le principe que Julius Peterson appelle réduction d'un cercle à un point, que l'on pourrait appeler, dans un vocabulaire plus proche de celui utilisé dans nos classes, de transformation d'une contrainte par translation : là où l'homothétie permet de supprimer une contrainte, la translation n'autorise simplement que de la transformer, et, par exemple, de transformer "tangent à un cercle" en "passant par son centre".

Lancer la figure ExpCT3C.fig d'expérimentation pour le plaisir des yeux

L'idée de Viète est donc d'ajouter ou de soustraire aux rayons des deux cercles qui ne sont pas les plus petits, le rayon du plus petit cercle. Dans le cas d'une construction en géométrie dynamique, il faut donc savoir à chaque instant lequel des trois est le cercle de plus petit rayon, et c'est ce que fait la première macro proposée en chargement. Ensuite, les cercles obtenus sont à modifier par homothétie afin de redevenir tangents aux trois cercles. Là encore, il faut s'assurer que la modification est bien faite d'une manière générale, pour tous les cas de figure.

Voyons cela en détail :

  À partir de trois cercles de base, on applique la macro de comparaison pour avoir les trois cercles logiques, notés C1, C2, C3 et en particulier le plus petit C1 (en orange) de centre O1.

On effectue ensuite le translaté du cercle C1 sur les droites des centres de façon à pouvoir ajouter et soustraire le rayon de C1 aux deux cercles C2 et C3 , ci dessus on a soustrait le rayon avec les cercles marrons, on l'a ajouté avec les cercles gris. Comme il y a 2 paires de deux cercles, on a 4 cas à traiter. Chacun produisant au maximum 2 cercles, on a donc au plus 8 cercles tangents aux trois cercles.

Détail du principe sur un premier cas.

Commençons par les deux cercles gris, cercles pour lesquels on a ajouté le plus petit rayon. En appliquant la macro qui construit les cercles tangents de même type à ces deux cercles et passant par le centre O1 de C1, on construit deux cercles intermédiaires comme ci-dessous (de centre I1 et I2).

Lancer la figure Viete1.fig intermédiaire précédente pour appliquer les macros ou Viete2.fig ci-dessous comme figure de départ.

Pour transformer ces deux cercles en des cercles tangents à C2 et C3, il faut définir correctement l'opération à effectuer car à priori, selon la position des cercles, tous les cas sont possibles. On pourrait croire par exemple qu'il faut retrancher le rayon de C1 à chacun des cercles quand il est tangent extérieurement au cercle intermédiaire, et il faut l'ajouter s'il est tangent intérieurement. C'est ce à quoi invite l'illustration ci-dessus. Or il faut être prudent car selon la taille ou la position des deux cercles de centre I1 et I2 on peut être amené à d'autres modifications. C'est la raison pour laquelle ici, on travaille de plus avec le point de contact rendu sur un cercle par la macro utilisée.

Construction effective

Dans ce cas la manipulation à effectuer est trés simple : on considère la demi-droite d'origine O2 - centre du cercle logique C2 passant par ce point de contact. Dans tous les cas - dans tous les cas - la modification à apporter consiste à prendre le cercle de centre le point correspondante (ici I1 puis I2 ) et passant par l'intersection de cette demi-droite avec le cercle logique C2 lui-même.
 

Un second cas

On continue, avec le cercle modifié marron (réduction du rayon de C1 ) pour C3 et l'autre modification (ajout du rayon de C1 en cercle gris) pour C2. En appliquant la macro qui construit les autres cercles tangents (de types différents, un intérieurement, l'autre extérieurement) à ces deux cercles passant par le centre de C1, on construit deux nouveaus cercles intermédiaires de centre I3 et I4. Comme précédemment, on utilise la transformation par demi-droite pour aboutir aux solutions 3 et 4 (en général, car elles peuvent ne pas exister pour certaines positions des cercles, on se placera toujours dans des illsutrations où les constructions existent).

 

Les deux derniers cas

 

On reprend la même démarche avec les deux dernièrs possibilités des cercles marrons et gris. Par exemple dans le cas où l'on réduit le rayon des deux cercles, c'est-à-dire quand on cherche un contact avec les deux cercles marrons. On utilise la macro donnant les cercles tangents de même type.

 

Figure finale dynamique du problème d'Apollonius

Lancer la figure VieteSol.fig terminée. On peut observer des situations trés diverses, comme :

Charger la macro CTgt3C.mac correspondante.

Remarques :

1 - la méthode naturelle pour les problèmes de contact reste l'inversion.
2 - Une autre méthode classique consiste à travailler à partir des axes radicaux des cercles.

 

Une première utilisation : coniques à centre de foyer F passant par 3 points A, B, C.

Le cercle directeur associé au foyer F est un cercle tangent aux trois cercles de centres respectifs A, B et C passant par F. L'application de la macro précédente donne 4 cercles solutions. On peut ainsi construire les 4 coniques répondant à la question avec une macro qui construit une conique connaissant son foyer et le cercle directeur, ci dessous de même couleur que leur cercle directeur.

la macro CnkFC1.mac déjà vue sur les coniques convient. On obtient alors :

 

Lancer la figure CnkF3PBi.fig correspondante.

 

Remarques :

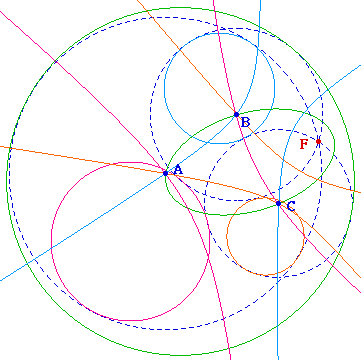
1 - En terme de Cabri-construction, les quatre coniques sont en fait huit car on utilise effectivement les 8 cercles, selon la position des points. Par exemple il y a - en terme de construction - deux coniques de chaque couleur.

2 - En réalité, il n'y a bien que 4 solutions. On peut le construire plus "correctement" avec Cabri par une approche monofocale : il est facile de construire les 4 directrices ... qui elles ne seront pas 4 droites parmi 8.

Lancer la figure CnkF3PMo.fig correspondant à la remarque ci-dessus ou encore consulter la version monofocale de cet exercice.

 

 

 [U1 - cercles tangents à une droite et passant par 2 points] [U2 - cercles tangents à un cercle et passant par 2 points
[U3 - cercles tangents à deux cercles et passant par un point]

[Résultats généraux] [Axe radical] [Théorème de Pascal]
[Exercices sur la puissance et les axes radicaux] [Retour Géométrie 2D]

 

Menu général