Image de deux droites orthogonales

TAOrtho1.fig

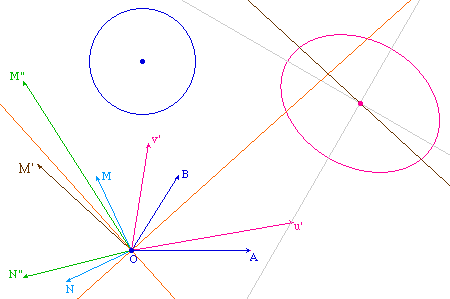
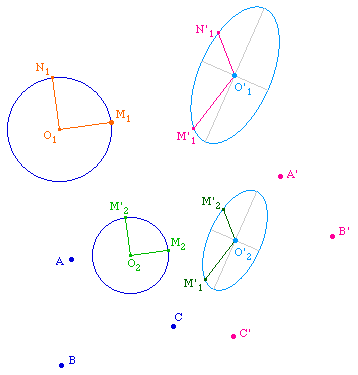
On sait que l'image, par une transformation affine (TAff), de deux droites orthogonales sont deux droites sécantes, en général non orthogonales. Ci dessous, dans la TAff qui envoie ABC sur A'B'C' on a construit l'ellipse de centre O'1, image d'un cercle de centre O1 et les images O'1M'1 et O'1N'1 de deux rayons orthogonaux O1M1 et O1N1 du cercle initial. Pour illustrer que la propriété est vectorielle, on applique la même construction à un second cercle, avec des rayons parallèles aux premiers. Les axes des deux coniques sont tracés par une macro indépendante ( AxesHE.mac de la page Axes par point de Fregier ) On observe tou d'abord que les axes des deux ellipses sont parallèles (respectivement) et donc que leurs directions est une propriété vectorielle liée à la TAff. On peut par exemple déplacer le centre O2 du second cercle pour observer que les directions des axes restent les mêmes. Or la donnée d'un cercle et d'une conique est aussi celle d'une forme quadratique - dont la conique peut être considérée comme la ligne de niveau q(x) = 1 - dans un espace vectoriel muni d'un produit scalaire - dont le cercle est la ligne de niveau 1. Le théorème de diagonalisation simultanée dit justement qu'il existe une base orthonormale pour le produit scalaire qui est orthogonale pour la forme quadratique, c'est-à-dire ici, puisque nous somme dans le plan affine, qu'il existe deux rayons orthogonaux d'origine O1 qui auront pour image deux rayons conjugués portés par les axes, comme on peut l'observer ci-dessous :

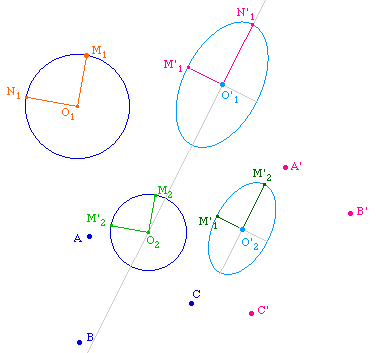
Autrement dit, nous venons d'illustrer, pour le plan affine, le résultat suivant : Pour toute application affine d'un espace euclidien, il existe une base orthonormale dont l'image est une famille orthogonale. Ici comme nous sommes en dimension 2 et que l'on s'intéresse aux bijections affines, on peut traduire plus simplement en : Pour toute transformation affine du plan, il existe un couple de directions orthogonales qui ont pour images deux directions orthogonales.

Détermination de ces directions

Le résultat théorique - montré plus loin - que nous illustrons ci-dessous est le suivant :

Si on note f l'application vectorielle associée à une transformation affine, et f* son endomorphisme adjoint. Alors f*of est trivialement un endomorphisme symétrique, et donc diagonalisable dans une base orthonormée. L'image d'un repère affine orthonormé est orthogonal si et seulement si il est dirigé par une base de diagonalisation de f*of.

TAOrtho2.fig

Dans la figure illustrée ici, on considére une transformation affine qui envoie OAB sur O'A'B' (non visible ici) qui correspond à la bijection vectorielle f transformant la base (OA, OB) en (u, v). L'image du cercle est l'ellipse. Pour un vecteur OM on construit OM' le vecteur image par f et OM" l'image de OM par f*of, en utilisant les macros réalisées dans la partie Algébre linéaire du site. Avec ces macros on peut en particulier construire aussi les directions propres de f*of (en orange ci-dessus).

On a ensuite tracé la parallèle à (OM') passant par le centre de l'ellipse.

Cette construction permet d'illustrer que quand OM et OM" sont colinéaires, la parallèle à (OM') passant par le centre de l'ellipse devient l'un des axes de l'ellispe : les vecteurs propres de f*of sont les directions dont les images sont les axes de la conique.

Comme on a aussi tracé un vecteur ON orthogonal à OM, on voit que son image ON" est colinéaire à ON ssi OM" l'est à OM : on pourrait par exemple illustrer ainsi que la base de vecteurs propres de f*of est bien orthogonale, même sans savoir concrètement construire les directions propres d'un endomorphisme comme nous l'avons fait ici.

Remarque : Cette construction illustre ausi que le grand axe de l'ellipse est associé à la plus grande valeur propre.

Preuve du résultat

Soit (e₁, ..., e_n) une base orthogonale de E, R-ev de dimension n (au moins 2), et f un endomorphisme de E. On cherche une caractérisation sur cette base pour que les f(e_i) soient orthogonaux. La notation (.|.) désigne le produit scalaire.
On remarquera que si un vecteur de la base est dans le noyau de f, son image est orthogonale à tout vecteur.

1 - Si la base est formée de vecteurs propres de f*of, il est clair que les f(e_i) sont orthogonaux car (f(e_i) | f(e_j)) = (e_i |f*of(e_j)) = (e_i |k_je_j) où k_j est la valeur propre associée à e_j. Donc est nul si (e_i | e_j) l'est.

2 - Réciproquement, si l'image de la base est une famille orthogonale, pour un élement e_j donné, on a, pour tout i, (f(e_i) | f(e_j)) = 0, soit (e_i |f*of(e_j)) = 0. Et donc, soit f*of(e_j) = 0 est alors e_j est vecteur propre de f*of associé à la valeur propre 0, soit l'hyperplan H =<e_i>_i‚j engendré par les n-1 vecteurs de la base différents de e_j est l'orthogonal de <f*of(e_j)>. Cela signifie alors que f*of(e_j) est colinéaire à e_j (écriture sur la base) et donc que e_j est vecteur propre de f*of. Ainsi, dans les deux cas, e_j est vecteur propre de f*of.

D'où le résultat : l'image d'une base orthogonale par une application linéaire est une famille orthogonale ssi elle est constituée de vecteurs propres de f*of.

En particulier, pour les transformations vectorielles (et affines) en dimension 2, il existe un unique couple de directions orthogonales dont les images soient de directions orthogonales.

Menu général