Forme polaire associée à une conique

Forme polaire d'une forme quadratique
1 - construction de la forme polaire

Forme polaire associée | Exploration sur l'orthogonalité | Application à la dimension 3

[Groupe linéaire] [Réduction des endomorphismes] [Adjoint d'un endomorphisme] [Diago. simultannée]

Etant donnée une conique, on peut la considérer comme la ligne de niveau q²(x) = 1 pour une forme quadratique q. On s'intéresse ici aux formes quadratiques non dégénérées, et donc aux coniques à centre. En particulier le plan affine est vectorialisé en le centre de la conique, et on identifie ainsi un point du plan affine au vecteur dont il est l'extrémité.

La ligne de niveau q²(x) = 1 équivaut à q(x) = 1 ou q(x) = -1. Et donc, dans le cas de l'hyperbole, il faut lui associer son hyperbole conjuguée, pour la ligne de niveau q(x) = -1.

Construction de q(x) pour x quelconque

FPol01.fig (traite uniquement de l'ellipse - voir plus loin pour l'hyperbole)

Construction de la forme polaire f(x,y) = [q(x+y) - q(x) - q(y)]/2

FPol02.fig

FPol02b.fig ou FormePol.mac (pour les ellipses)

Cabri-test sur la symétrie de la forme associée

Si la symétrie est contenue implicitement dans l'écriture de la forme polaire, on peut toutefois faire la vérification ci-contre (avec Cabri-confirmation du parallèlisme) d'une part pour vérifier la construction. D'autre part, il peut être interessant en formation de montrer comment un nouvel outil comme Cabri incite à des vérifications différentes : pour savoir si M et N ont même abscisse dans (O, u) et(O, v), on s'intéresse au parallélisme des droites associées.

FPol03.fig

Le cas de l'hyperbole

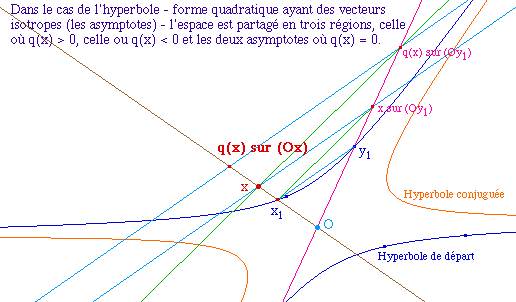
FPol04.fig (contient les deux cas ellipse et hyperbole) ou HypConju.mac

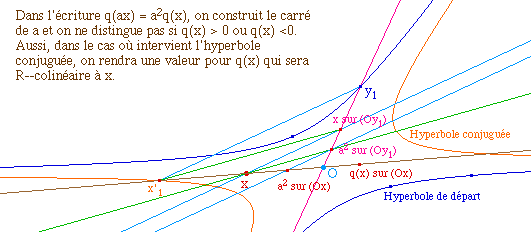
Norme.mac (voir l'aide)