 |
|
4 - Cas des points symétriques
[1 - Aspect historique] [2 - Preuve du théorème] [3 - Cas des céviennes] [5 - Cas des points doubles]
[6 - L'isotomie] [7 - Le cas de la parabole] [8 - Utilisation avec le cercle] [9 - Exercices sur la configuration de Carnot]
[Retour "Considérations affines et projectives"] [Retour Coniques] [Menu Général]
 |
|
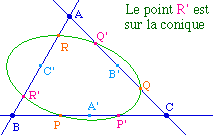 |
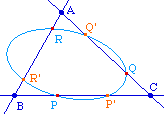
Il résulte ainsi du théorème de Carnot la propriété suivante :Théorème : Soit ABC un triangle. On considère trois points P de (BC), Q de (CA), et R de (AB) autres que les sommets du triangle, et P', Q', R' les symétriques de P, Q et R par rapport aux milieux respectifs des côtés du triangle. Alors les six points sont sur une même conique.
|
 |
|
|
|
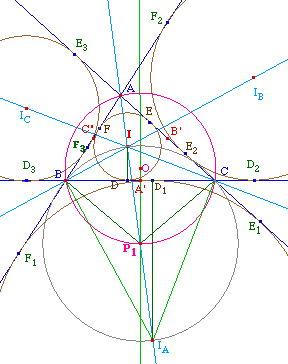
Remarque : l'argumentation proposée ici vaut pour la géométrie euclidienne puisque l'on utilise des résultats angulaires de cocyclicité et la conservation des milieux par projection. Or, cette propriété de symétrie est aussi vraie dans un contexte hyperbolique, alors que les deux arguments utilisés ne le sont pas. Il serait intéressant de chercher une preuve purement métrique, applicable dans un contexte non euclidien.
[6 - L'isotomie] [7 - Le cas de la parabole] [8 - Utilisation avec le cercle] [9 - Exercices sur la configuration de Carnot]
[Retour "Considérations affines et projectives"] [Retour Coniques]