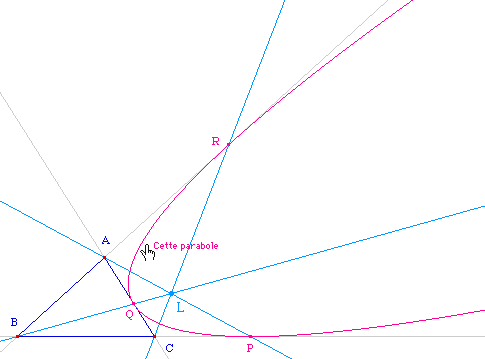
Expérimentation :
![]() CarPar01.fig
(déplacer L, on a toujours une parabole)
CarPar01.fig
(déplacer L, on a toujours une parabole)
7 - Le cas de la parabole
[1 - Aspect historique] [2 - Preuve du théorème] [3 - Cas des céviennes] [4 - Cas des points symétriques]
[5 - Cas des points doubles] [6 - Céviennes et points isotomiques] [8 - Utilisation avec le cercle] [9 - Exercices sur la configuration de Carnot]
[Retour "Considérations affines et projectives"] [Retour Coniques] [Menu Général]

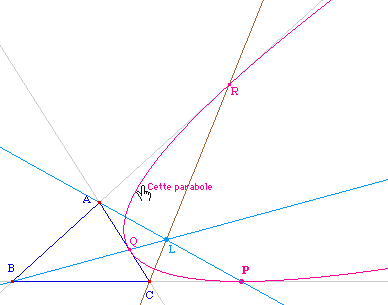
Expérimentation :
![]() CarPar01.fig
(déplacer L, on a toujours une parabole)
CarPar01.fig
(déplacer L, on a toujours une parabole)
Construction par calcul barycentrique - Construction par des considérations projectives - Expérimentation sur le lieu du point cévien -Preuve barycentrique du résultat précédent - Preuve algébrique
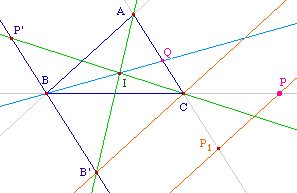 |
P étant donné, on cherche à construire Q tel que - en mesure algébrique - QC/QA = PC/BC. On peut procéder comme ci-contre : projection selon (AB) pour obtenir B' (définitif) et P1 intermédiaire. P1 donne P' par translation.L'homothétie qui transforme B' en A et P' en C transforme alors B en le point Q cherché.On en déduit la figure ci-dessous.
|
|
|
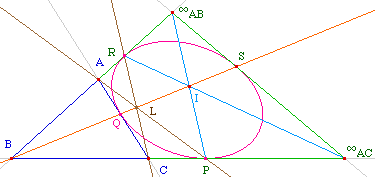
On construit les parallèlogrammes BPIR, CQJP et ARKQ. On trouve comme coordonnées barycentriques :
et comme coordonnées tangentielles :
|
|
|
Donc les droites (BI), (CJ) et (AK) sont concourantes ou parallèles. |
|
Nous allons montrer que dans le cas où la conique est une parabole, ces trois droites sont parallèles.En effet, la conique est une parabole ssi elle est tangente à la droite de l'infini en un point S. En raisonnant dans le triangle BIABIBC, on voit que les droites (BS), (IABP) et (IBCR) sont concourantes en un point I. (IAB désignant le point à l'infini dans la direction (AB))Dans le plan affine, BPIR est le parallèlogramme évoqué plus haut, et (BI) est alors la parallèle à l'axe de la parabole - lieu des centres en projectif). De la même façon, les droites (CJ) et (AK) sont ausi parallèle à l'axe de la parabole, et ainsi les trois droites (BI), (CJ) et (AK) sont parallèles quand la conique est une parabole, comme illustré dans la figure ci-dessus (réciproque pour l'équivalence dans le calcul analytique suivant ?). |
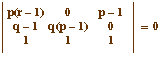 |
Traduction analytique : les droites sont parallèles ssi le déterminant ci contre est nul soit ssi q(1-p) = 1, ce qui est le résultat obtenu à la partie précédente, on peut en déduire la même construction. |
Construction par calcul barycentrique - Construction par des considérations projectives - Expérimentation sur le lieu du point cévien -Preuve barycentrique du résultat précédent - Preuve algébrique

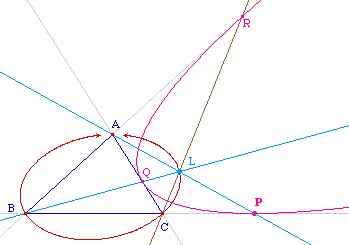 |
Le lieu du point de concours L est une ellipse passant par les trois sommets - privée de ces 3 points.Quelques expérimentations simples montrent facilement que c'est l'ellipse de Steiner circonscrite au triangle.Pour une vérification expérimentale, on s'intéresse donc à la construction réciproque (ci-dessous) où L est un point de l'ellipse de Steiner circonscrite, construite par 5 points, en utilisant simplement que son centre est le centre de gravité du triangle.La vérification avec Cabri est aisée :avec la macro "conique par 2 tangentes leurs contacts et un point on construit la conique à partir du point L, et Cabri confirme que c'est toujours une parabole. |
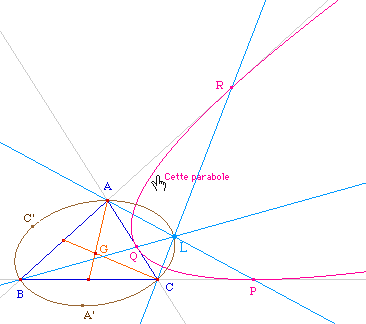
Pour une vérification expérimentale on peut reprendre la figure précédente et redéfinir le point L comme point de base.
Construction par calcul barycentrique - Construction par des considérations projectives - Expérimentation sur le lieu du point cévien -Preuve barycentrique du résultat précédent - Preuve algébrique
[1 - Aspect historique] [2 - Preuve du théorème] [3 - Cas des céviennes] [4 - Cas des points symétriques]
[5 - Cas des points doubles] [6 - Céviennes et points isotomiques] [8 - Utilisation avec le cercle] [9 - Exercices sur la configuration de Carnot]
[Retour "Considérations affines et projectives"] [Retour Coniques]