|
|
Soient P et P' de (BC), Q et Q' de (CA), R et R' de (AB), différents des sommets.Alors les six points P, P', Q, Q', R et R' sont sur une même conique ssi :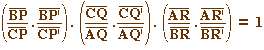 |
|
2 - Preuve du théorème - Cas impropres - Première application
[1 - Aspect historique] [3 - Cas de céviennes] [4 - Cas des points symétriques] [5 - Cas des points doubles]
[6 - L'isotomie] [7 - Le cas de la parabole] [8 - Utilisation avec le cercle] [9 - Exercices sur la configuration de Carnot]
[Retour "Considérations affines et projectives"] [Retour Coniques] [Menu Général]
|
|
Soient P et P' de (BC), Q et Q' de (CA), R et R' de (AB), différents des sommets.Alors les six points P, P', Q, Q', R et R' sont sur une même conique ssi :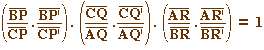 |
|
On suppose ici connu le résultat affine suivant : par 5 points distincts, il passe toujours une unique conique. Il en résulte que l'on peut considérer ce théorème comme une caractérisation de la "co-conicité" de 6 points 2 à 2 sur 3 côtés d'un triangle.
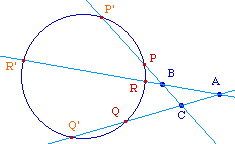 |
|
|
|
|
Les coniques impropres sont soit l'ensemble vide, soit réduite à un ou deux points, soit deux droites, parallèles ou sécantes. Ici, comme on traite de coniques passant par 6 points, dont au moins trois distincts car appartenant à des côtés différents d'un triangle, les seuls cas impropres envisagés sont les cas où la conique dégénre en deux droites.
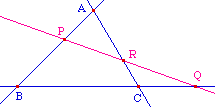 |
|
Dans le sens direct, il résulte du théorème de Ménélaüs que si 6 points sont alignés par trois sur deux droites, ils vérifient la relation de Carnot qui est donc vraie pour les cas impropres envisagés. Récipoquement ...
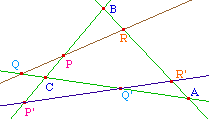 |
|
Nous ne traiterons plus désormais que des cas de coniques "propres", c'est-à-dire ellipse, parabole ou hyperbole..
Si un hexagone a ses côtés opposés parallèles, alors il est inscrit dans une conique.
Voir aussi la preuve barycentrique classique
|
|
On prolonge les côtés de l'hexagone pour obtenir le triangle ABC dans lequel on peut appliquer le théorème de Thalès (6 fois pour obtenir les 6 rapports de la relation de Carnot).Ainsi a-t-on
|
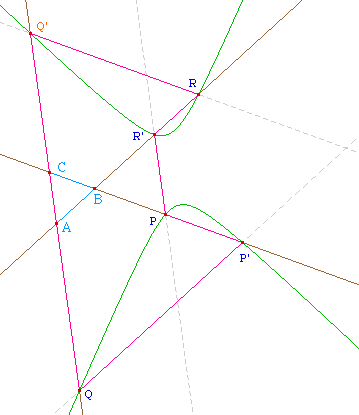
Autre illustration dans une configutation non croisée, non convexe
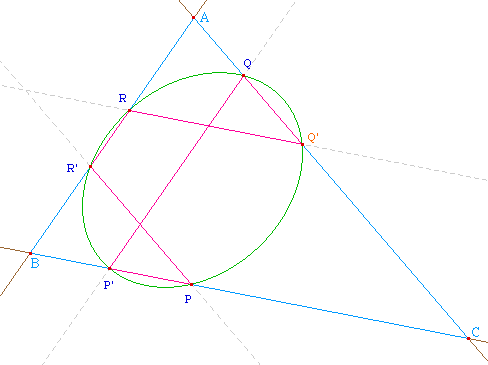
Illustration dans une configuration générale croisée
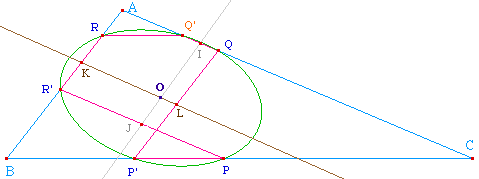
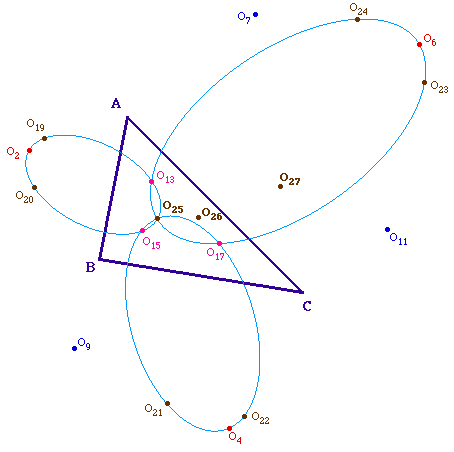
Pour une illustration claire
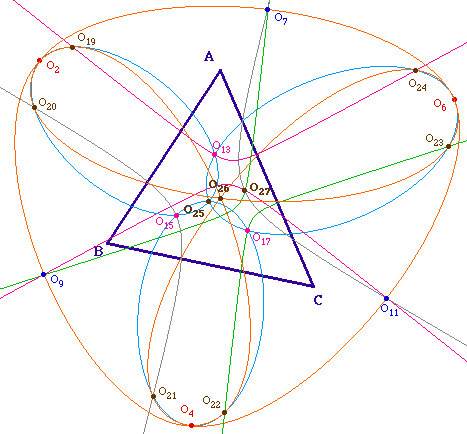
Pour une illustration plus complète
[6 - L'isotomie] [7 - Le cas de la parabole] [8 - Utilisation avec le cercle] [9 - Exercices sur la configuration de Carnot]
[Retour "Considérations affines et projectives"] [Retour Coniques]