

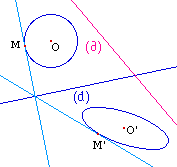
Comme transformation affine, la
symétrie oblique transforme le centre d'un cercle en
le centre de l'ellipse, conserve le contact. C'est une
application involutive. En chargeant la figure, on peut
vérifier avec Cabri qu'elle conserve les aires (car
de déterminant -1). On peut aussi vérifier
expérimentalement que les axes de l'image d'un cercle
ont des directions fixes. En plaçant le centre du
cercle à l'intersection de la base et de la
directrice de la symétrie, on trouve
expérimentalement ces directions fixes.
![]() SymOblik.fig.
SymOblik.fig.
|
|
On généralise la symétrie oblique en remplaçant le point à l'infini correspondant à la direction par un point O, à distance finie. La droite (OM) coupe l'axe (d) en H, M', l'image de M, est le point tel que M et M' soient conjugués harmoniques de O et H. Cette transformation s'appelle l'homologie harmonique de centre O et d'axe (d).
|
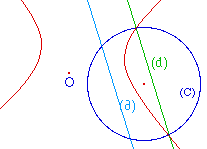
Si l'homothétique de (d)
coupe le cercle en deux points,
la transformée est une hyperbole.![]() NatTrfHE.fig
pour les cas de l'hyperbole et de l'ellipse.
NatTrfHE.fig
pour les cas de l'hyperbole et de l'ellipse.
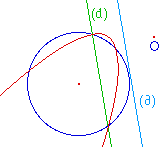
Si l'homothétique de (d)
est tangente au cercle,
la transformée est une parabole.![]() NatTrfP.fig
pour le cas spécifique de la parabole.
NatTrfP.fig
pour le cas spécifique de la parabole.
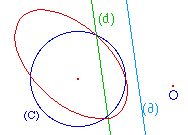
Si l'homothétique de (d) ne
coupe pas le cercle,
la transformée est une ellipse.Justification de cette
dernière règle
Elle provient du fait qu'en
géométrie projective, une conique coupe la
droite de l'infini en 2 points (hyperbole) 1 point
(parabole) ou aucun (ellipse). On peut donc regarder ce
qu'il se passe pour la conique de départ - ici le
cercle, mais cela pourrait être une conique - avec la
transformée, dans l'homologie harmonique, de la
droite de l'infini (la droite "delta" indiquée plus
haut ). On se ramène ainsi à des
considérations affines.
On notera également que si
le cercle passe par le centre de l'homologie, sa
transformée passe aussi par ce point, en étant
tangente au cercle.
|
|
Dans le cas de l'hyperbole, soit L une intersection du cercle de base - éventuellement de la conique de base comme illustré sur la figure ci-contre - avec l'homothétique de l'axe. Notons L' l'intersection de la tangente au cercle en L et l'axe (d) de l'homologie. Alors la parallèle à (OL) passant par L' est une asymptote de l'hyperbole . On construit de même l'autre asymptote avec l'autre point d'intersection.
|
|
|
Le centre de l'homologie est un (le) foyer de la conique et l'homothétique de l'axe (d), dans l'homothétie hO,1/2 est la directrice associée.On peut en faire une vérification expérimentale en utilisant un résultat classique sur les tangentes aux coniques (ou une caractéristique des directrices et foyers) :Si on considère la tangente à une conique en un point M et T son intersection avec la directrice associée au foyer O, alors l'angle en O du triangle MOT est droit.
|
|
|
|