

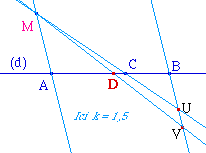
A, B, C sont trois points d'une
droite (d), k est un réel, M un point du plan
n'appartenant pas à la droite (d). La droite (MC)
coupe la parrallèle à (AM) passant par B en
U.
![]()
La droite (MV) coupe (d) en un point D. Ce point est
indépendant de M. On dit que le birapport (A, B, C,
D) est égal à k. On a :
![]()
![]() BiRapp.fig.
BiRapp.fig.
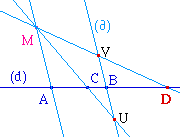
Si k=-1, on dit que D est
conjugué
harmonique de C par rapport
à A et B.
Autrement dit, on a : ![]()
Le cas particulier k=-1 est important de part la
symétrie qu'il introduit. Ainsi D est
également conjugué harmonique de C par rapport
à B et A, mais aussi C l'est de D par rapport
à A et B (ou B et A). De même A et B sont
conjugués harmoniques l'un de l'autre par rapport
à C et D.![]() DivH.fig.
DivH.fig.
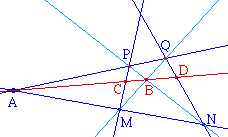
Le cas du quadrilatère
complet
Dans cette configuration, (A,B) et
(C, D) sont en division harmonique. Etant donnés
trois points alignés A, B, et C, la configuration du
quadrilatère complet donne un procédé
de construction d'un quatrième point D tel que C et D
divisent harmoniquement le segment [AB].
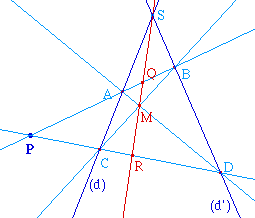
Etant données (d) et (d')
deux droites sécantes en S et P un point distinct de
S, on mêne deux droites issues de P cooupant (d) et
(d') respectivement en A, B et C, D. Soit le point M
d'intersection de (AD) et (BC). Le lieu de M quand les
droites (AB) et (CD) varient est une droite passant par S,
applelé polaire
de P par rapport à (d)
et (d').
D'après le paragraphe précédent, P et Q
sont conjuguès harmoniques par rapport à A et
B; de même P et R le sont par rapport à C et
D.![]() PolDrte.fig.
PolDrte.fig.
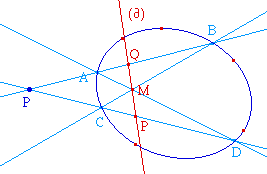
Comme pour deux droites, on
définit la polaire d'un point par rapport à
une conique de la même façon. On a encore les
couples (P, Q) et (A,B) en division harmonique, de
même que (P, R) et (C, D).
Réciproquement, pour toute droite (d) du plan, il
existe un point P appelé
pôle
de (d) par rapport à la conique tel que (d) soit la
polaire de P par rapport à cette conique.
Les points de d'intersection entre la polaire de P et la
conique, quand ils existent, sont
les points de contact des
tangentes à cette
conique issues de P, ce qui donne un (autre)
procédé de construction des tangentes à
une conique.![]() PolConik.fig.
PolConik.fig.
Manipulation possible
: Observer la position de la
polaire par rapport à la conique quand on
déplace P.
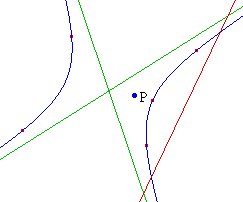
L'extérieur d'une hyperbole
est donc, parmi les deux parties qu'elle délimite,
celle qui contient son centre. On observera les
propriétés suivantes :
Si un point P extérieur à une hyperbole est
dans la région comprise entre l'hyperbole et ses
asymptotes, la polaire coupe l'hyperbole en deux points de
la même branche.
Si P est extérieur dans la partie
délimitée par les deux asymptotes, la polaire
coupe l'hyperbole en deux points appartenant à des
branches différentes.
Enfin si P est sur une asymptote, la polaire est
parallèle à l'autre asymptote.![]() AsymHyp.fig
AsymHyp.figLa construction des asymptotes est
proposée à la prochaine page.