

|
|
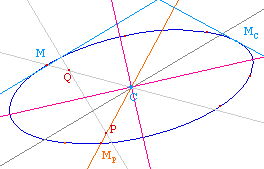
Le lieu de Q quand M décrit la conique est une hyperbole équilatère passant par P et C appelée hyperbole d'Appolonius associée à (C) et à P.
|
|
Tout d'abord Q est en P pour M sur le diamètre (CP), et que Q est en C pour un point M tel que (CP) soit une direction de normale à la conique (M en MC sur la figure).Pour M aux sommets de la conique, les droites (CM) et la perpendiculaire au diamètre conjugués sont parallèles, le point Q est rejeté à l'infini. Cela signifie que les asymptotes de l'hyperbole sont parallèles aux axes de la conique : l'hyperbole d'Appolonius est donc équilatère.
|
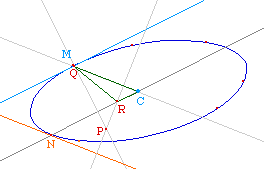 |
Dans le cas de l'ellipse, si on construit un second point R de l'hyperbole d'Appolonius à partir d'un point N sur le diamètre conjugué de (CM), P étant sur deux hauteurs du triangle CQR, il en est l'orthocentre, et ainsi, quand M varie, la droite (QR) reste perpendiculaire à la direction fixe (CP).
|
|
|
Par construction même de l'hyperbole d'Appolonius, ses éventuelles intersections avec la conique sont les pieds des normales menées de P à la conique.Il peut y avoir jusqu'à 4 normales à une conique issues d'un même point P, et il y en a toujours au moins deux.
|
|
|
Théorème de
Joachimasthal :
|
|
|
Cas de l'ellipseOn considère le rectangle circonscrit à l'ellipse passant par ses sommets. Les droites issues de P perpendiculaires aux diagonales de ce rectangle recoupent l'autre diagonale aux points U et V. Le centre O de l'hyperbole d'Appolonius associée à P est le milieu de [UV].
|
|
|
Si on considère un point M de l'ellipse et que P soit redéfini comme point sur objet de la normale à l'ellipse en M, alors on peut observer que :Le lieu des centres de l'hyperbole d'Appolonius des points d'une normale à l'ellipse est une droite.
|
|
|
Cas de l'hyperboleDans ce cas, l'hyperbole d'Appolonius associée à un point P passe, en plus du centre C de l'hyperbole, par les porjections orthogonales U et V de P sur les asymptotes à l'hyperbole.Le centre de l'hyperbole d'Appolonius est le milieu de [UV].
|
|
|
On peut observer la même propriété que dans le cas de l'ellipse :Soit un point M de l'hyperbole et P redéfini comme point sur objet de la normale à l'hyperbole en M, alors :Le lieu des centres de l'hyperbole d'Appolonius des points d'une normale à l'hyperbole est une droite.
|
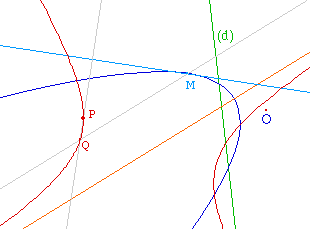
dans l'illustration ci-contre O
et (d) sont |
Dans ce cas le centre est à l'infini. Q est donc l'intersection de la perpendiculaire en P à la tangente en M à la parabole et de la paralléle à l'axe passant par M - qui fait office de droite (CM) le centre étant à l'inifini dans la direction de l'axe.Le lieu de Q est encore une hyperbole équilatère. Elle est asymptote à l'axe de la parabole.
|
|
|
L'hyperbole d'Appolonius et la parabole peuvent avoir 3 points d'intersection, ce qui donne au plus trois normales à la parabole issues de P.Le cercle circonscrit à ces trois points recoupe la parabole en son sommet qui est, comme dans le cas du théorème de Joachimsthal des coniques à centre, le point "diamétralement opposé" du point à l'infini dans la direction de l'axe de la parabole.
|