
|
|
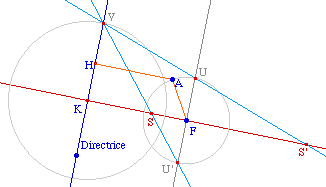
M est alors un point de la ligne de niveau MF/MP = e, ligne de niveau qui est un cercle centré sur (PF) dont on peut facilement construire le diamètre [RT] sur cette droite.En effet, S vérifiant la relation DF/DK = e, la parallèle en S à la directrice (KP) coupe (FP) en R qui vérifie aussi RF/RP = e. On construit de même T à partir de S'.Le centre I du cercle se projetant orthogonalement au milieu de [SS'], appartient à la médiatrice D' de ces deux points. |
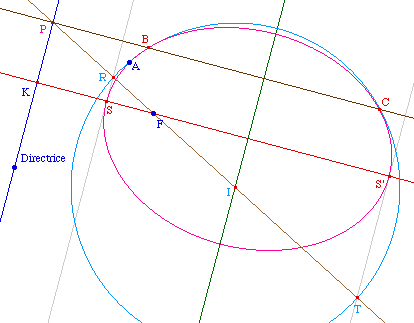
Partant d'un point B de la conique, on construit P sa projection orthogonale sur la directrice. La droite (PF) coupe l'axe non focal - constructible dès le départ comme médiatrice de [SS'] - en un point I. La tangente à la conique en B est la perpendiculaire à (BI) en B.
